The Nature of propulsion force and the Energy of the Future

Many things are beyond our scope of understanding not because of our poor reasoning power, but because of the narrowness of our scope.

What will, or what should be the energy of the future? What natural phenomena and processes will be at its bottom line? At what level of matter organization should one look for these phenomena and processes? These questions increasingly trouble the scientists engaged in exploring the new sources of energy, new means of its production.

Traditional means of energy production, for example, electricity, are known for their use of kinetic energy obtained from the wind, heated steam or pressure of falling water. In the first and second cases, it’s pressure difference which causes propulsion force, in the third case – it’s the force of gravitation. To obtain pressure difference artificially one has to use energy, burn fossil or nuclear fuel at power plants. Hydroelectric power stations require no fuel of course, as they are using a natural force of propulsion. Let’s examine the origin of this force and assess a possibility of designing its artificial analogy.

Little is known of the nature of the force of gravitation applied to experimental bodies. Lots of hypotheses exist, but the question remains: what mechanism creates propulsion force causing bodies to fall? What exactly causes the body to react by its free fall?

Note: experimental body, a body whose potential is too small to disturb the outside field.

1. If it’s the field which ‘catches’ body m and then ‘drags’ it toward the earth’s surface, what’s the mechanism of this?

2. Could the field be exerting its influence on body m if the body stayed unaffected by the field’s presence? If body m is to react, then why?

3. Is the cause of free fall entirely external, or there are some changes taking place inside the body?

4. What is to change inside the body so as make it move?

Rhythmodynamics views bodies as systems of interacting synchronous elements (oscillating experimental bodies) situated in a wave medium, the medium which has a propensity to carry periodic disturbances and propagate them with constant speed.

All principles are examined in the case of the least possible elementary system (fig.1) made up of two oscillating elements linked together by the standing wave.

Fig.1. The system has no reason to move in the wave medium because positions of the sources-oscillators and potential holes (nodes) coincide. The system is internally balanced.

The standing wave, being a disturbed state of the medium, plays the role of a common platform for the elements. Although this platform is floating in the wave medium, it’s also rigid, because the system’s elements, engaged in exchange of the wave energy, create potential holes and thereby fix each other there at a set distance.

The elementary system coming under pressure of internal or external factors may develop phase or frequency displacements which break wave synchronism and upset the existing balance.

Balance [equilibrium], a state created by the forces of a different vector cancelled out so that the system’s properties remain unaffected.

Dynamic balance [dynamic equilibrium], a process in which the controlled system develops in such a way which prevents significant deviation of the system from the set trajectory caused by the medium disturbances.

The upset balance results in the shift of potential holes relative to the system’s elements (fig.2). If synchronism is not restored and it becomes permanent the system seeks to adapt to the new state. One of the means is for the elements to drift in the wake of the shifting potential holes. If the system has phase displacement the internal balance is restored if the speed of the moving elementary system and the phase displacement have the following relation:

(с – velocity of waves propagation)

i.e.

* The dependence of speed on phase displacement was confirmed by experiment with oscillating floats in the water pool. The break of synchronism made the system of floats move.

Fig.2 Phase displacement leads to the shift of potential holes (the nodes of the standing wave) relative to their initial position, and consequently, to the position of the sources (oscillators). The internal balance is broken. The sources come under the influence of the wave field, and naturally will drift toward their potential holes.

No matter what the origin of the disturbances is, man-made or natural, anyway, they lead to the processes aimed at restoration of synchronism and elimination of the imbalance of internal forces triggered by the disturbances. In a free of the fields space, the break of synchronism occurs due to external impact, say, of material forces which leads to the change of speed regime. In the field of gravitation, the break of synchronism is triggered by the field, and compensated by a free fall.

When we examined the mechanisms leading to the accelerated fall, we assumed that oscillators (oscillating experimental bodies), being on their own, do not react to the field of gravitation by their motion, whereas the systems of interlinked oscillators do react. But in such case of actual gravitation, one can assume that the least element of the manifest matter is the one which doesn’t react to the field. For example, if proton, or some other particle, falls in the gravitational field, it cannot be regarded as the least possible element of the manifest matter, but it could be regarded as a system of such elements.

The implemented research [1,2] has made it possible to conclude that it was not the gravitational field which was acting as a force of propulsion but the changes which the field triggers inside the body. These changes are of phase nature and lead to a changed dynamics of linkage, to asynchronism between the elements of the body which breaks internal balance, and consequently, leads to the body reacting as a system to the emerging changes. This reaction is based on the propensity of oscillating systems to seek the state of synchronism. In other words, a model was created expounding the mechanism of formation of the propulsion force which actually accomplishes the body’s fall in the field of gravitation.

What’s important there is understanding that the force of propulsion is an intrinsic quality of the body as a system, its reaction to external gradient conditions. If gravitational field didn’t change anything in the body the body would have no reason to react to the field. The same way, say, dielectric fails to react to a strong magnetic field (practically nothing changes in the dielectric) while a body of iron does react.

Major question rises there: is it possible to artificially influence the interatomic synchronism of bodies so as to trigger the reaction of a system of atoms in the form of a directional propulsion force?

Yes, theoretically it is possible. But it’s a long way to go from theory to practice. As a first step, let’s try to understand what processes and at what level of matter organization are responsible for the force of propulsion.

Quantum reality in the macro-world phenomena

Classical reality emerges from quantum reality provided there is interaction between the micro-objects. So far there is no unified description of classical and quantum realities, though everyone knows that such description is not simply possible, it’s necessary.

Here’s a simple way of describing the macro-world phenomena (inertia, motion, propulsion force, gravitational force, kinetic and potential energies, centrifugal force) relating to classical mechanics through the notions and means of electrodynamics and quantum mechanics. In effect, we are talking about a new quantum-mechanical interpretation of the formulas of classical mechanics.

The first such interpretation became possible after the creation of rhythmodynamic model of the processes which trigger the motion of macro-bodies in space [1].

Rhythmodynamics (RD), a branch of science studying the role of periodic processes in the formation of natural phenomena and their qualities.

The notion of ‘motion’ is known to be present in all formulas of classical mechanics, in one form of the other. There are several kinds of motion but we’ll focus on only two of them: the motion with constant speed (by inertia), and the motion with constant acceleration (free fall).

According to [1]

 ,                                  (1.00)

i.e. the speed of the body is proportional to the phase displacement between the body’s oscillating elements.

One of the main achievements of rhythmodynamics was finding this relation, the formula of which reflects the processes without which the above-mentioned regimes of motion in wave medium would hardly be possible. Relation 1.00 is the main element of the new way of description of macro-phenomena. It sets a tentative, so far, link between classical and quantum mechanics. From a mathematical point of view, it’s simply a different formulation and interpretation of the laws of classical mechanics. From a physical point of view, we are talking of a qualitatively new vision of the world.

1. Force and acceleration in the field of gravitation

There are several options of deriving the relation describing the body’s free fall in the field of gravitation. Option 1 seems most curious because it originates from the well-known premises.

Option 1 (gravitational red shift)

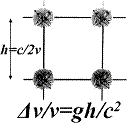
Einstein predicted phenomenon of gravitational red shift. In earth conditions such shift is insignificant, but they did manage to measure it in an experiment based on the Mossbauer effect.

If a photon with frequency  is emitted at height Н above the surface of the Earth toward its center, at the Earth’s surface level its kinetic energy  increases at the expense of potential energy. Following the law of conservation of energy we formulate:

  (1.01)

It assumes that photon’s mass  is constant. So, the receiver encounters a photon with frequency , different from the one it had during its emission by the source. With Н=10 m

Fig.3 In a three-dimensional body one can always find some atoms which are farther from the earth’s surface, and others which are closer.

But what, in the Earth’s gravitational field, will the frequency difference be of similar (fig.3) vertically positioned atoms, with the distance between them of one standing wave, i.e. ?

              (1.02)

                           (1.03)

If frequency difference does depend on acceleration g, then it would be possible to state that it’s the frequency difference which forms acceleration. Let’s rewrite formula 1.03 relative to acceleration g:

                                      (1.04)

                                      (1.05)

There are other ways of obtaining relation 1.05 (one of them is rhythmodynamic) which corroborates the derived dependence of acceleration on frequency difference. Substituting acceleration g in formula   by its new expression, we obtain a new meaning of the notion the force of gravitation:

,                                           (1.06)

but

Then

                                   (1.07)

In 1.07 the force of gravitation applied to the experimental body is proportionate to the frequency difference imposed by gravitational field on the interacting atoms.

Option 2 (rhythmodynamic)

According to classical mechanics:

                                              (1.08)

According to rhythmodynamics:

 ,                                  (1.00)

but ,

i.e.а                                  (1.09)

or                                    (1.05)

where:

V – velocity of the system of oscillators

с – velocity of the waves in the medium (speed of light)

а, g – acceleration of the system of oscillators

 – phase displacement between oscillators

 – oscillators’ frequency difference

For    

Gravitational field imposes a frequency difference on the body’s oscillating elements, thus breaking the system’s natural synchronism. This happens at least at the atomic level of matter organization and leads to the system’s reaction in the form of the body’s self-propulsion with acceleration.

Self-propulsion, internally provoked natural change of the system determined by its contradictions indirectly reflecting external factors and conditions.

2. Wave interpretation of the force of gravitation

Quantum mechanics, a branch of physics studying the ways of description and the principles of motion of elementary particles, atoms, molecules, atomic nuclei, as well as macro-phenomena. Quantum mechanics determines relations of quantities describing particles and systems with the physical quantities directly evaluated in the experiment.

Let’s examine an experiment measuring the force of gravitation affecting an experimental body m. But what triggers this force? The researcher is convinced that the force affecting body m is nothing but a net reaction of the body’s elements to the conditions created by the gravitational field in and around the body (gravitational field makes space heterogeneous). But what exactly changes inside the body, what parameters, and why does the body react to the changes?

Classical mechanics asserts that in the gravitational field body m comes under the effect of force

                                            (1.06)

Earlier it was shown that gravitation g is proportionate to the gravitational red shift, i.e.

,                                       (1.05)

where the frequency difference can be expressed through the speed of light and wave lengths:

  (2.01)

Then

,                       (2.02)

and

(2.03)

But quantum mechanics accepts as true the relation:

,                                           (2.04)

then

      (2.05)

Taking into account 2.05, we’ll rewrite 2.02 and 2.03

,                                 (2.06)

and

.                            (2.07)

But , and ,   

then

,                               (2.08)

or 

 or          (2.09)

where:

h – Planck’s constant

p – wave impulse

E – body’s overall energy

The left part of formulas 2.07, 2.08, 2.09 has a classical expression of force, while their right part –  a quantum-mechanical expression.

Expressing through the notions and parameters of quantum mechanics () we’ve shown the link between quantum and Newtonian mechanics. In effect, 2.09 is a wave equation revealing a frequency-wave nature of force in general, and gravitational force in particular.

3. Kinetic and potential energies

Kinetic energy, a measure of bodies’ mechanical motion which depends on velocities of their motion in a given inertial frame of reference.

Potential energy, forces hidden in matter which could become effective under certain circumstances.

Considering dependence of speed on phase shift one can take a different look on the notions of kinetic energy and potential energy.

                                         (3.01)

but

                                          (3.02)

then

  (3.03)

where:

then

   (3.04)

  (3.05)

The difference between formulas 3.03, 3.04, 3.05 and formula 3.01 is that their right part reflects directly the gradient-phase nature of kinetic energy, i.e. inner system processes which ensure the presence of such energy. In other words, the phase shift reveals the cause of the system’s propensity to move. If such system is blocked its kinetic energy should be viewed as potential energy seeking to be transformed into kinetic one. Such system has an inner propensity to move, and the energy which actualizes it is called potential energy. Transformation of potential energy into kinetic one takes place if the system is no longer blocked.

If ,  the energy is kinetic, i.e. present in the body and maintaining its motion:

                               (3.03)

If , ,  i.e. the system is blocked, the very same energy (3.03) is potential:

                               (3.06)

The common mechanism-cause of kinetic and potential energies lies in the presence of internal phase changes. These changes, if free motion is obstructed, reveal themselves in the form of internal force of propulsion (as propensity to move).

Now we have a deeper understanding of the processes responsible for kinetic and potential energies.

4. Centrifugal force

Centrifugal force, a force with which a material particle moving uniformly on a circular trajectory affects the link.

                                       (4.01)

But                                     (4.02)

then

  (4.03)

   (4.04)

5. Quantity of motion

Quantity of motion, a measure of inner propulsion force maintaining velocity regime in a wave medium. (Rhythmodynamic interpretation).

                                             (5.01)

but                                     (4.02)

then

                                  (5.02)

According to the motion equation, phase displacement makes the body (system) move at a speed corresponding to this phase displacement. If the body’s (system’s) free motion is obstructed, the force it will exert on the block will be:

 (5.03)

Analyzing the obtained expression of force one can see that the change of the system’s velocity regime may be not due to external force, but due to the phase-frequency state of the system’s oscillators. In that case propulsion force emerges, bringing the system in a state of sustained motion.

                 (5.04)

6. Velocity of the energy flow

Suppose we have two sources of waves whose frequency, respectively,  and  (fig.4), with .

Fig. 4. The observer must move to implement the condition of equal frequencies of the incoming waves and energies emitted from the sources. In this case he registers a standing wave! The energy flow of the standing wave is equal to the wave’s velocity.

In the moving observer’s reference frame we have:

                                 (6.01)

                                (6.02)

But , therefore

                  (6.03)

Let’s solve the equation relative to the system’s velocity , in which equality of incoming frequencies and a regular standing wave is observed:

(6.04)

The same, relative to the emitters, is also the speed   of the flow of energy concentrated in the standing wave:

                                 (6.05)

7. Rhythmodynamic and  quantum-mechanical interpretation of the formulas of classical mechanics

The familiar formulas of classical mechanics (1) have acquired rhythmodynamics (2) and quantum-mechanics’ interpretations. What’s important is that the new formulas of classical mechanics have acquired fundamental constants (the speed of light and Planck’s constant), as well as basic parameters used in electrodynamics and quantum mechanics (phase, frequency, wave impulse). The formulas are compiled in Table 1.

Table 1

The new interpretation allows us to take not the usual formal, but a fresh look at the phenomena and their properties through processes which contribute to the formation of these phenomena and properties. This is a new approach and a new depth of understanding natural phenomena.

The new formulas often contain a relation  numerically equal to  and usually marked as:

In which case some formulas acquire a more compact form, for example:

,

,  

,   

Conclusions and consequences

The expressions we’ve derived for speed, acceleration, the force of gravitation, kinetic and potential energies, centrifugal force, quantity of motion in their essence contain the elements of quantum mechanics and electrodynamics which points to the phase-frequency causal nature of these phenomena. The new formulas could well replace or go side-by-side along the old ones, especially if we need to switch from one system of notions and ideas to the other.

Actually, we’ve examined a nonconfrontational means of producing motion where an artificially induced phase asynchronism becomes a force of propulsion. This is a sort of Baron Munchausen effect in physics in which the control over the phase balance brings the system out of the state of internal equilibrium, making it self-propel. While in normal conditions the state of the system’s equilibrium exists when the system’s center of mass coincides with the point where the internal net force equals zero, any change in the phase correlation between the system’s elements shifts this ‘zero’ point relative to its former place, i.e. relative to the initial center of mass. As a result the balance of internal forces shifts too, which is also accompanied by the shift of the energy carcass relative to the elements (atoms) which produced this carcass (fig.5). This shift is countered by the system, reacting in the form of self-propulsion. The normal example of such reaction are bodies affected by the field of gravitation.

Fig.5. Emergence of the phase displacement leads to the shift of the energy carcass, disbalance of internal forces which is countered in the form of self-propulsion.

In the field of gravitation, the force of propulsion exists in its pure form as the body’s reaction to asynchronism which the field imposes on the body’s elements. Gravitational field changes and rigidly maintains the changed parameters, ‘freezing’ them in such a way which leaves the body no other option but motion toward the source of the field. If the body is prevented from motion by force, its pursuit of the state of synchronism is to manifest itself in the form of the constant exertion of force on the impediment. In such case they refer to the potential energy and the force of propulsion the origin of which is the field’s changing and ‘freezing’ body parameters (3.06).

But is it possible to artificially change and retain the changed parameters? Are there any obstacles to it, and if there are, what are they?

There are many ways to artificially form gradients of parameters, for example, by uneven heating, but it’s not yet known how to retain the obtained changes in a state we want. The main obstacle to this is absence of the absolutely rigid bond between the elements of matter, i.e. in a material system the elements always have certain degree of freedom allowing them to neutralize the incoming negative changes, for example, through relocation or re-crystallization. In effect, this ability is the main obstacle to producing the force of propulsion. Artificial ‘freeze’ might help there denying the system’s elements all degrees of freedom except those which produce the force of propulsion. For instance:

Suppose we had a body suspended in the field of gravitation. Suppose the gravitational field changed the correlation of phases between the body elements in such a way as to produce a directional force of propulsion. If the achieved correlation of phases in the body were now ‘frozen’, i.e. artificial means of preventing restructuring under changing conditions were used, the force of propulsion would remain in the body even if the gravitational field were to disappear. This is not a science fiction: the wave equation’s solution for the simplest oscillating systems directly indicates to such propensity of those systems.

It’s worth noting that there are objects in nature which have an inherent force of propulsion, like binary molecules of gas or liquid made up of atoms of close isotopes: О₂=¹⁶О+¹⁷О, N₂=¹⁴N+¹⁵N, Н₂О=¹Н+¹Н+¹⁶О, Н₂О=²Н+¹Н+¹⁷О etc.). Intuition suggests that such molecules have asymmetric energy (fig.2, fig.6), and therefore they should either decompose, or somehow escape this asymmetry, through motion, for example.

Fig.6. Examples of energy distribution in the internal and external space. The sources (left) have frequency displacement; the sources (right) have phase displacement. In the first case the system is expected to propel, in the latter – to rotate.

In effect, we’ve raised the question of the source of kinetic energy of isolated molecules in which the imbalance of internal parameters responsible for the interaction of the elements and the system’s integrity makes them react. Self-propulsion is one of the forms of such reaction. The law of the conservation of energy is not broken there because the system (a disbalanced molecule) is using self-propulsion only as a means of overcoming its ‘internal problems’.

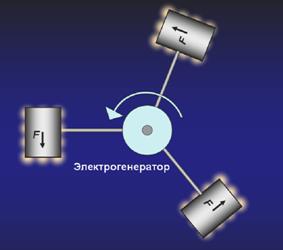
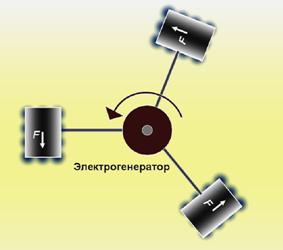
Fig.7. A schematic diagram of the source of energy made up of an electric generator and material objects with ‘frozen’ phase shift.

As for the future of energy production, creation of the force of propulsion by means of parameters’ ‘freeze’ or through energy asymmetry, though look fantastic (fig.7) like anything radically new, still deserves serious attention. Mastering these means would make it possible to obtain any necessary quantity of motion and energy in any place in the Universe without any violation of the law of conservation of energy.

We do not know yet how to ‘freeze’ bodies in the necessary state, but we have at least reached understanding of what’s to be done. If Nature can, why cannot we? Which means a new line of research has emerged. The initial steps in such direction have already been taken.

MIRIT Scientific-Technological Center

Academician of the Russian Academy of Natural Science

Yuri N. Ivanov.

December 13, 2008.

Bibliography:

1. Ivanov Y.N. Rhythmodynamics. New Center Publishers, 1997.

2. Ivanov Y.N. Rhythmodynamics.  Energy Publishers, 2007.

3. Physical encyclopedia. Sovetskaya encyclopedia, 1990.

4. Blekhman I.I. Vibtrational mechanics. Nauka, 1994.

Books [1] and [2] are freely accessed at http://www.mirit.ru

P.S. The means of the energy production expounded in this article is a distant perspective, now visible only in theory, but sooner or later we’ll master them (if we don’t destroy ourselves prior to this). Our closest perspectives are hydrogen and magnetic energy. But even there you cannot manage without a new vision of the inner-matter processes, without new understanding of the physics of natural phenomena.

We all know too that sooner or later mankind would have to switch to alternative sources of energy because someday we’ll be hit by real (not the present imaginary) energy crisis, which is likely to be caused not by the depletion of the fossil fuels, but by our inability to extract them due to the global geo-catastrophe. Which means that the question of new means of the energy production should be put at the top of our current agenda without delay!