|

 |
Fig.7
1. Phase shift is absent. V=0 – no transfer in the
medium. Interference field emerged, as well as the standing wave
between the oscillators. 2. Phase shift is absent.
Orientation to the transfer in the medium is perpendicular . The
speed of transfer V=0.75c. Direction of transfer is from left
to right. Interference field is compressed. Additional anti-nodes
and nodes areas have emerged . The distance between the standing
wave nodes has diminished.
Fig.10. Phase shift is
absent. Orientation to the movement direction is parallel
(oscillators move from left to right). Motion speed V=0,75c. |
|

 |
Fig.11. Spider effect.
Fig.111 If frequency
discordant system is restrained a spider-like interference pattern
emerges. That’s why this phenomenon is called a ‘spider-effect’. |
|


 |
Fig.12. The system of
coherent oscillators on the plane. The outward wave radiation is
practically absent. But this radiation may become manifest at a
certain distance away from the system, which implies that unless you
know about its source, the energy in wave medium will be emerging as
if from ‘nowhere’. |
|

 |
Fig.20.a Distribution of
wave energy from numerous sources (left model) moving at a
supersonic speed (12 Max). Similar process also takes place in the
supersonic jet streams. |
|

 |
Fig.19 In a supersonic
cone of a single oscillator a standing, relative to the source,
field of wave energy emerges. The velocity of this field equals
precisely the velocity of the source (V=1,5c), i.e. the field
moves with the source. A picture made from space shows a running
wave pattern in the boat’s wake. |
|

 |
Fig.20. That’s how the
field of distribution of wave (interference) energy looks produced
by two supersonic coherent oscillators. The velocity and direction
of the field movement equal precisely the velocity and direction of
the oscillators V=1,5c. The start of ‘Proton’ rocket. The
energy nodes and anti-nodes are clearly visible in the supersonic
jet stream. |
|


 |
Fig.38. Along the line
drawn between the oscillators the outward emission is absent (V=0,
Df
=0)
Fig.39 Inner balance has
been broken. Outward emission has emerged (V>0,
Df
=0).
Fig.40 Thanks to the
changes made (V>0,
Df
=pi*V/c)
the inner balance of the system has been restored. |
|

 |
Fig.45 Energy
distribution pattern: a) dipole b) triangle. |
|
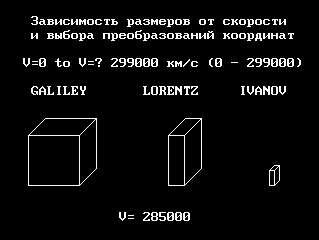 |
Fig.54 Velocity of a
package of standing waves V=0 Dimensions of a package of
standing waves with V=0,9ñ
Fig.56 While the objects
approaching the speed of light turn, according to Lorentz, into
‘flying pancakes’, according to Ivanov they turn into dots. |
|
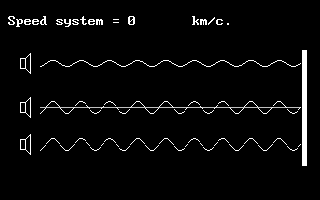 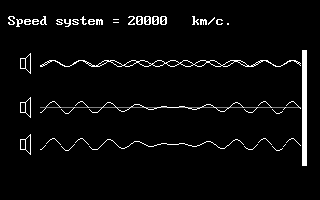 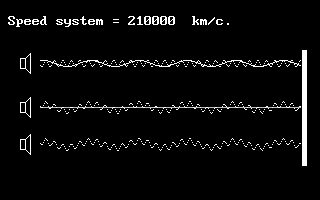 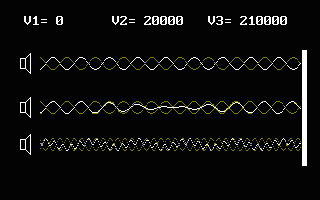 |
Fig.25 a) direct and
counter waves; b) wave superimposition: instantaneous show of
resultant; c) developing in time the resultant outlines in space a
picture with well-defined anti-nodes and nodes, i.e. the standing
wave.
Fig.24 That’s how a
computer model looks in which the oscillations’ source is presented
as a speaker. The direct and counter-waves have equal frequencies
but different velocities, and therefore different lengths. Addition
of these waves results in the beat. If this process is examined as
summed up in time, the nodes and anti-nodes will be visible which
allows one to speak of a standing wave.
Fig.57 Emitters’
frequency is constant. With the device’s velocity increase relative
to medium, and in accordance with Doppler’s rule, the direct and
counter waves change their lengths.
For the inside observer in the system which changed speed the
frequencies of these waves will remain equal
but the nature of interference is to change, which is to lead to
contraction of distance between the neighboring nodes, standing wave
length change, and increased number of standing waves. The package
of standing waves compresses.
|
|


 |
Fig.68 Phase
displacement leads to the shift of nodes and anti-nodes.
Fig.69 The observer has
to move to implement the condition of frequency equality of the
waves coming to him. In this case he registers the standing wave!
Fig.70 Frequency difference
takes place (v1>v2).
The speed of energy flow and the speed of the car are equal. The
passengers in the car observe a standing wave, and for them the
energy transfer doesn’t exist. The observers outside see a complex
wave picture which is not a standing wave.
Fig.71 Frequency
difference is absent. The flow of energy in the system of motionless
observers is absent. In the system of moving observers relative to
standing wave the energy flow exists. The of energy flow velocity
equals in modulus the car velocity. Could it be the source of de
Broglie waves? |
|

 |
Fig.72
Two sources of waves are in the nodes of the
standing wave they’ve created. The nodes are areas of stable balance
for the sources. In these areas the gradient of the wave field
energy is absent.
Fig.73.
Attempts to bring the wave sources closer, i.e.
to take them out of potential’s holes, lead to the reaction of the
standing wave aimed at bringing the sources apart. The reaction
lasts till the sources are again in the balance areas.
Fig.77
Moving away from the center under the influence
of the pulling apart forces, the sources will soon form another two
standing waves and slide into new nodes, i.e. new areas of stable
balance (potential’s holes). |
|

 |
Fig.82
Phase displacement between oscillators is
Df
=45grad
(V=0) which made the standing wave move right. |
|
 |
Fig.85
Df
=0grad,
V=0,25c. |
|
 |
Fig.86
Areas of stable (potential’s holes) and unstable balance. |
|

 |
Fig.97 Phase
displacement triggers the shift of potential holes relative to their
initial position, and appropriately, the shift of sources. The
sources are influenced by the wave field so their natural reaction
would be motion toward potential holes. If such motion is not
obstructed the sources will be moving until they find themselves in
the areas of stable balance.
For the sources to be again in potential holes
with the standing wave anti-node between them, the system must pick
a certain velocity V. |
|

 |
Fig. |
|
 |
'Spider.s
Network' - Interference from three sources.
Asymmetrical
cellular structure deformed by arrhythmia is
observed. Such a system
will strive for self-motion to the left
|
 |
Fig.107 The greater
phase displacement is, the greater is the relative shift of
oscillators and nodes. |
 |
Fig.116
In gravitational field relative to the restrained system of wave
sources, potential holes are shifted toward the field source
(a). If restraining factor is removed the system starts moving
because the sources will be seeking to catch up with the shifting
nodes (b). Free fall in gravitational field is characterized by
absence of internal deformations in the system (c). |