“Since
nature is a principle of motion and change, and since our
inquiry is about nature, we must not overlook the question
of what motion is. For without understanding motion, we
could not understand nature.”
Aristotle
RHYTHMODYNAMICS
Second edition, revised and extended.
By Yuri N.
Ivanov
MOSCOW 2007
Ivanov Yuri Nikolaevich.
Rhythmodynamics. – M:
ISBN
978-5-98420-018-9
Significance of scientific theory is determined by its
ability not just to explain logically and clearly what and how happens, but
also to show the ways and means of practical application of those ideas the
theory expounds. That’s where rhythmodynamics beats all modern hypotheses,
theories and paradigms as it reveals the essence, the mechanism of basic
phenomena and shows how the new understanding can be applied in concrete areas.
The new revised and extended version of Yuri Ivanov’s
book gives a definite model account as to: how systems self-organize; what
inside-matter processes trigger and maintain the bodies’ motion by inertia; how
bodies in gravitational field form their propensity to free fall; what energy
flow is; what the speed of this flow is and what it depends on.
A new understanding of space dimensions is given; the
notions of ‘amplitudeless’ and ‘frequency’ space have been introduced and defined;
coordinate axes of these dimensions have been introduced too. A possible cause
of red shift among distant objects in the Universe (Alice’s effect), and the
cause of self-propulsion of isolated molecules are examined.
Besides, interpretation of the results of the famous
Michelson’s interferometer experiment is given which is based on the ‘standing
waves’ compression’ phenomenon. Application aspects concerning energy
production and new ways of motion in space are inspected.
Rhythmodynamics surprising compatibility with other
scientific approaches is explained by the absence of unfamiliar or vague
notions and ideas in its foundation. Waves and wave sources are present more or
less in all known theories of physics, therefore all the effects, phenomena and
laws described y rhythmodynamics are automatically true in those theories.
The book is provided with a DVD containing films, a
library of rare books, teaching materials and demonstration programs.
About the author: Yuri N. Ivanov, Doctor of
Science, Academician of the Russian Academy of Natural Science, Director
of the scientific-technical center STC "MIRIT"
(Rhythmodynamics
site:
www.mirit.ru).
Publishing house ‘Energia’, Moscow
ISBN
978-5-98420-018-9
©
Yu. Ivanov 2007
Table of
Contents
|
Introduction. . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
From the author . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Rhythmodynamics
(RD) : its goals and tasks . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . .
Chapter 1.
The
Elements
(12)
§ 1.01
On dogmas, axioms and postulates in
physics . . . . . . . . . . . . . . . .
. . . . . . . .
§ 1.02
The choice of instruments
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
§ 1.03
Axiom of foundation-regularity. . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . .
§ 1.04
Wave geometry . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
§ 1.05
The properties of the wave geometry
objects . . . . . . . . . . . . . . . .
. . . . . . . . .
§ 1.06
The wave geometry potentials
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§ 1.07
Rhythmodynamics: postulates . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . .
§ 1.08
Establishing the tasks to be solved . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .
Chapter 2.
Interference
(49)
§ 2.01
Is it possible to manage without the
notion of wave medium? . . . . . . . . . . .
§ 2.02
Standing wave. The basic properties we
know as well as new ones . . . . . .
§ 2.03
Oscillations, standing waves, and
physical standards of measure. . . . . .
. .
§ 2.04
Dimension’s contraction and Michelson’s
experiment . . . . . . . . . . . . . . . . .
§ 2.05
RD interpretation of the results of
Michelson’s experiment . . . . . . . .
. . . . .
§ 2.06
The speed of light in one direction . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .
§ 2.07
RD transformations of coordinates . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .
§ 2.08
Lively standing wave . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
§ 2.09
Frequency difference and the speed of
energy flow . . . . . . . . . . . . . .
. . . . .
§ 2.10
On nature of electric current . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . .
Chapter 3.
Fundamentals
of Self-organization
(107)
§ 3.01
Energy as a measure of motion .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§ 3.02
Absolute and relative aspects of energies .
. . . . . . . . . . . . . . . . . . . . . . . . . .
§ 3.03
Self-organization of wave systems
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§ 3.04
Self-organization and phase displacement
.
. . . . . . . . . . . . . . . . . . . . . . . . . .
§ 3.05
Kinetic energy . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . .
§ 3.06
Wave model of elastic object . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . .
§ 3.07
Properties of artificial elastic bodies . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . .
§ 3.08
Inertia is the property of system . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
§ 3.09
Model view on self-propulsion of
molecules . . . . . . . . . . . . . . .
. . . . . . . . . .
Chapter 4.
Motion (135)
§
4.01 Motion as a fundamental
property . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .
§
4.02 Translational motion . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
§
4.03 The nature of the
moving force . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
§
4.04 Three states of
quiescence . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . .
§
4.05 First state of
quiescence . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . .
§
4.06 Second state of
quiescence . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . .
§
4.07 Third state of
quiescence . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . .
§ 4.08
Specifics of RD
modeling . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . .
Chapter 5. Force, gravitation
(153)
§
5.01 Nature of force . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . .
§
5.02 Motion in gravitational
field . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . .
§
5.03 Equation to calculate
acceleration in gravitational field . .
. . . . . . . . . . . . . .
§
5.04 Force of gravitation . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
§
5.05 Comparing formulas
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .
§
5.06 Gravitation and
frequency pulling (hypothesis) . . . .
. . . . . . . . . . . . . . . . . . .
Supplement (166)
1.
Scientists’ opinions
about this work . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .
2.
Science:
privatization of truth . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . .
3.
The number of space
dimensions . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
4.
Space expansion and
the Alice’s effect . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . .
5.
Comparison of the RD
and classical mechanics formulas . . . . . . . . . . .
. . . . .
6.
Action without
counteraction . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . .
7.
Rhythmodynamics and
vibrational mechanics . . . . . . . . . . . . . . . . . . . . . . . . .
8.
Phase-frequency
tension and gravitational metrics . .
. . . . . . . . . . . . . . . . . . .
9.
Black Holes
(phase-frequency interpretation) . . . . . . . . . . . . . . .
. . . . . . . . . . .
10.
About Louis de
Broglie’s law of phase harmony . . . .
. . . . . . . . . . . . . . . . . . .
11.
Rhythmodynamics’
place in physics . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . .
Conclusion: results and perspectives . . . .
. . . . . . . . . . . . . . . . . . . . . . . . .
Bibliography
. . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
5
8
10
12
20
27
29
32
35
46
48
49
50
60
73
77
92
97
98
100
105
107
107
109
113
118
121
124
128
129
136
137
142
144
146
147
150
151
155
157
161
163
164
164
166
166
169
172
174
175
182
184
188
203
213
215
218
|
Back to contents ↑
Introduction
Truth is one of the ways of distorting reality!
In 1980s lots of
science fiction films usually began like this: “In the year 2015…” after which
achievements of the earth civilization were shown, namely ability of a free
space travel, not just to the neighboring planets but to the far corners in the
Universe. Conviction grew that this would become true. Unfortunately, the
qualitative breakthrough in science and technology has failed to materialize
for several reasons. One of them is that there is still no reasonable
explanation of fundamental natural phenomena, and there’s no knowledge of the
nature of processes which form these phenomena. There are few of them: motion,
inertia, force, gravitation, nature of the fields, nature of electricity and
elementary particles. These phenomena and their properties are still
considered inherent and therefore require no explanation. But not all think so.
May be for this reason opinion was circulated that discovery of the physics
aspect of these phenomena is beyond the ability of human mind, the same way
understanding of the easiest technical appliance is beyond the mental abilities
of a dog.
With such
attitude to human capabilities one can hardly expect any qualitative
breakthrough in science. Therefore dilemma emerges: either to quietly sanctify
one’s own inaptitude, i.e. declare the modern view of the world final because
any other views will never emerge, or to admit frankly one’s own inaptitude,
and run the risk of being fired, or wait for a messiah who might clarify
everything in science. This second coming is actually expected in science; they
even revived the practice of fighting dissent there, the so-called committee
against pseudo-science. But this is a different issue.
In 1997 a book
called ‘Rhythmodynamics’ was published in which the author expounded the
results of many years of research of fundamental problematic phenomena. Ten
years since lots of additional experiments have been conducted which confirm
the conclusions and predictions made in the book.
The new edition
presents Rhythmodynamics as a method of examining the processes which form
phenomena and their properties. The author would like to stress that
Rhythmodynamics is not claming the role of a universal paradigm, but it can be
quite useful instrument in solving complex tasks in theoretical and applied
science. For example, the means of rhythmodynamics helped visualize the process
of gravitation formation by the imposition on the elements which make up the
body of the oscillators matching the elements in phase and frequency. Interference
pattern in the form of a spider-effect has become an illustration of
gravitational field impact on a system of two linked atoms. A way to achieve
anti-gravitation has been predicted. An interesting formula was drawn up
determining acceleration of material system in gravitational field at the
expense of discordance of phase and frequency triggered by this field. Eureka!
Another example
of rhythmodynamics effectiveness is visualization of assumed interatomic
processes which form self-propulsion of isolated molecules, like Í2Î. This self-propulsion could well be
the cause of Brownian motion.
Special
attention was paid to the physical phenomenon which the author calls
‘compression of standing waves’. This phenomenon was discovered in 1981 after a
theoretical analysis of interference processes in Michelson’s device. It was
discovered that to explain the negative result in Michelson’s experiment one
had to take into account the wave nature of matter and to base the change in
interferometer’s dimensions on the property of standing waves to compress with
speed increase, i.e. on actual physical phenomenon. Such approach makes
unnecessary all speculations about invariancy, as well as the postulates of the
constancy of the speed of light, of space filled with void, ether attraction and
lots of others.
In author’s
opinion, the achievements made in metrology could soon make it possible to
stage an experiment in determining the speed of light in one direction, the
results of which could help physics get rid of lots of ‘rubbish’ both in the
sphere of theory and scientific ideology.
Mankind requires
a clear-cut picture of the world, effective scientific instruments capable of
solving practical high level tasks for the sake of well-being of all society.
Wave geometry, a
separate branch of science in itself, was suggested as one of the instruments,
with the help of which a number of physical phenomena were discovered and processes
forming these phenomena were modeled. For example, a model was created of a
system of oscillators which has no outward radiation; amplitudeless way of
energy existence was shown; relation of speed and acceleration of the
oscillating system to phase-frequency shift between the system’s elements was
determined; the law of preservation of energy was examined and a new formula
was drawn up as a sum of its manifest and non-manifest components.
The issue of
multi-dimensional world possessing frequency depth was examined in this
book. A concept of frequency space was suggested, i.e. in our usual
system of coordinates a coordinate axis of frequency depth was
introduced. Such approach strengthens the argument in favor of the so-called
‘parallel worlds’ existing side-by-side with us in our single space but in different
frequency bands.
Rhythmodynamics
has made it possible to re-write the formulas of classic mechanics in such a
way that they acquired phase, frequency, speed of light and Planck’s constant
parameters. Isn’t it a firm indication toward the way of unification of
classical mechanics, elecrodynamics, and quantum mechanics? May be such
approach could help us make the first steps toward creation of a single
physics, in which macro- and micro-levels of matter organization, phenomena and
processes won’t be artificially divided?
List of the
main issues
On
fundamental phenomena:
1.
How exactly is the uniform and rectilinear
motion of a body in space (motion by inertia) is ensured?
2.
What is the origin of a body’s propensity to
resist external impact (inertia)?
3.
What is the origin of force, centrifugal and
gravitational? What processes trigger the emergence of centrifugal force during
the body’s motion along curvilinear trajectory? What changes in bodies does
gravitational field affect, and how exactly do these changes trigger
attraction?
4.
Through what and how does interaction between
‘elementary particles’ and macro-bodies take place?
5.
Can the physical essence of electric and
magnetic fields be comprehended? Can one understand the processes triggering
the energy flow, including the flow of electricity?
General
philosophical problems:
1.
What is container for everything possible which
exists, and what is it precisely filled with?
2.
What is the origin of continuum? Has continuum a
proto-element? Is continuum even and uninterrupted, or is it endlessly and
inwardly discrete?
3.
Presuming continuum is even, inseparable,
uninterrupted, how then can anything happen in it at all?
4.
Can anything exist in container provided
continuum has no proto-elements?
5.
Can one create a satisfactory view of the
universe without the notion of a ‘reality’?
The questions
of researcher’s consciousness and spiritual level:
1.
Who is the ‘customer’, the recipient of
information collected by the sense organs in the human body?
2.
In what form does the customer’s representative
resides in the body, and where is the customer himself?
3.
What does the customer need information for?
From the author
‘Everything that exists is justified in its existence’
Leibniz
Any phenomenon
or property is based on the processes which form them. It’s a general practice
in science to regard phenomena and their properties inherent until a theory and
instruments are created with the help of which such processes can be
discovered. For example, until the emergence of rhythmodynamics the notion of
‘gravitation’ was explained by the curvature of space or the flow of ether
toward matter. We understand that this could well be so, but we want
explanations to the curvature of space and ether flow. If they cannot be
explained, i.e. regarded as a ‘fact’, a hierarchy of hypotheses emerges in
which the unknown is explained by something yet more unknown. Which, in
science, is looked upon as a ‘mauvais ton’.
Another example
is motion, i.e. the bodies’ ability to move in space by inertia. Such motion is
regarded as inherent, i.e. something basic and preordained and therefore
requiring no explanations. And how about matter as a philosophical category?
How about physical fields as a special kind of matter, or rather special kind
of philosophical category?
With the
emergence of mathematics (all kinds of mathematics are based of arithmetic) it
became possible to determine correlations between the facts of micro and macro
worlds. Somehow this came to be regarded as a true physics. For example, the
rectilinear motion by inertia is characterized by speed
→
speed is determined by a ratio of a distance passed in a unit of time. The
question is what is the cause of motion? The answer is the cause of motion is
in the force which has been applied to the body!
Such answer
doesn’t reveal anything because the question referred not to the cause which
triggered motion, but to the cause of motion as a process, i.e. thanks to what
exactly the body moves in space in uniform and rectilinear way, what originates
and facilitates such motion? The modern physics doesn’t answer this seemingly
simple question.
In such case how
should one treat the now fashionable physical hypotheses about creation of the
universe, if we still do not know the origin of motion (there’s no matter
without motion…)?
The modern
interpretation of the main fundamental phenomena and properties sounds more
like a system of ritual chants rather than scientific explanations. Many
researchers are not content with this. They are forced to conduct their own independent
research so as to solve the problems which physics avoids to solve. As a result
of such research Rhythmodynamics emerged with the help of which model
analogies were created of those phenomena under study. If anyone succeeds in
creating a simpler way and means of explanation than I’ve created I’ll be much
obliged to this man.
Yuri N. Ivanov
Rhythmodynamics (RD): its goals and tasks
No image – no understanding!
There is a
problem in physics of explaining the processes which form the fundamental phenomena
and their properties. The problem is due to axiomatic nature of fundamentals
and, consequently, due to seeming absence of necessity of their in-depth
understanding, to say nothing of their visualization. But it’s the disclosure
of these processes which is essential for a qualitatively new understanding of
nature. Here Rhythmodynamics plays the role of an instrument for deeper
penetration, which gives qualitatively new knowledge by making its visual
presentation possible.
The term
‘Rhythmodynamics’ consists of two notions: ‘rhythm’ and ‘dynamics’.
RHYTHM
(Gk.rhythmos). An ordered recurrent alternation of some processes,
moments (acceleration and deceleration, tension and relaxation in motion or in
the course of something).
DYNAMICS
1. A branch of mechanics with deals with the motion of bodies under
the impact of forces applied to them. 2. A pattern or process of change of some
phenomenon. 3. Motion, action, development.
In which case,
RHYTHMODYNAMICS
(RD) is a branch of science studying the role of periodical
processes in formation of natural phenomena and their properties.
Specifically,
Rhythmodynamics, introducing in classical mechanics the notion of ‘wave medium’,
‘phase’ and ‘frequency’, using modeling and visualization of processes which
form the phenomena and their properties, makes it possible to deepen our
knowledge of them as well as discover so far unknown ties between the
fundamental phenomena regarded until then independent.
RD’s goals
and tasks
Goals:
·
research of natural phenomena and their
properties through creation of simple and illustrative means of their
presentation;
·
reaching understanding of processes
participating in formation of phenomena and their properties, starting from the
stage of their inception;
·
determining the adequacy of the drafted models
to the phenomena they are supposed to reflect;
·
a return to classical approach in physics, but
at a qualitatively higher level.
Tasks
outlined:
·
to form an illustrative user-friendly instrument
on the basis of Euclid’s geometry, arithmetic, algebra and trigonometry to
analyze and describe processes participating in the formation of phenomena and
their properties.
·
to verify the effectiveness of the instrument in
cases when the essence of mechanism of the most crucial notions, phenomena and
properties traditionally viewed as inherent is revealed.
Expected
result
To learn
something new is particularly difficult, especially if you are past school age.
So the best option is to introduce the RD elements into school text-books. For
example, the teaching materials (see DVD) already created could significantly
simplify the teaching and learning processes of some phenomena. Of course the
rival forces would do their best to ignore and block such knowledge. But the
book is already written! And it’s addressed to those who are not used in their
relations with reality to rely totally to established authority, to those who
at least tries to think independently, who sees that society as well as science
and its system of views are in a state of disorder and conflict, to those who
want to find out, understand and facilitate progress, i.e. make out life
better.
Rhythmus:
As if progress ever needed someone’s help! I’m sure
it will manage without any outside interference. The more so that instruments
for this are abundant – Galileo-Newton’s mechanics, Einstein’s theory, quantum
mechanics, a powerful calculus, brand new laboratories and technologies. Your
attitude might be more appropriate in the Age of Romanticism.
Dynamicus:
Are you trying to convince all, myself including, that
everything which exists in the world has already been discovered? Including the
nature of inertia, gravitation, nature of electricity, and so on and so forth?
I suspect you are simply trying to cover up the inability of modern science to
explain comprehensibly the most usual things. I suspect the commission to fight
the so-called pseudo-science was created exactly for this purpose of hiding
incompetence of certain personalities in science.
Back to contents ↑
Chapter 1. The Elements
Nothing exists except the continuum and the illusion
inside it!
Trying to
understand the “elements of this world” from the position of sound reason and
natural science, our minds are confronted with a paradox which is neither
possible to fully define, nor grasp. In other words, one cannot understand it,
but one can get used to it!
Back to contents ↑
§ 1.01 On dogmas, axioms and postulates in physics
What’s the world
we are living in built with? What were the elements used? The modern physics
cannot give a definite answer. Many scientists know this, some even openly
admit it.
In this case,
let’s put the question differently: Does the world really look the way the
modern physics present it? Does the modern physics portray the world as it is,
or does it portray the researches’ subjective notions of it?
The researches
study and portray the real world, but within the limits of their own subjective
abilities. Which means that the modern physics does not reflect the world as it
really is, and therefore gives a subjective view of what objectively exists.
The physical picture of the world is subjective because it’s based on the
subjects’ ability, their inner means (their senses, consciousness) of
reflecting the reality.
The absence of
at least one sense organ, or possession of an extra one unknown to us, has a
significant impact on our physical picture of the world. To understand it just
imagine yourself possessing hearing in the world of the deaf, or having sight
in the world of the blind.
Which implies
that physics created by a group of subjects of the same mind and perception is
in no way better than other physical concepts created by those subjects whose
perception and thinking differ somewhat. In both cases their physical concepts
will be subjective. Which means the society may have more than one school of
scientific thought, alternative world outlooks and ways of world exploration.
Let’s examine
the differing views on the issue of ‘continuum’ held by different groups of researches
of varying world outlook.
·
Democritus and Aristotle stated that continuum
consists of the continually dividable particles: “Continuum is what dividable
in parts, which are, in turn, dividable again”.
·
The continuum of the Eleatic school represented
by Xenophanes, Parmenides and Zeno is opposite to the continuum of Democritus
and Aristotle. Their philosophy is based on the Single, or Absolute Being.
Their main postulate: Being is eternal, and the continuum is endless,
consisting of neither divisible or indivisible parts.
The modern
science has adopted the Aristotle’s interpretation of the postulate-axiom of continuum.
It’s easy to explain the mobility of the ‘whole’ as all endlessly dividable
parts move one against the other. This is an easy and instinctively comprehensible
option, though in this case the answer must be given to the question of the
continuum’s proto-element.
It’s much harder
to explain the mobility of the world we observe if we postulate the continuum
as endless and indivisible. By definition, such continuum cannot afford even
the slightest shift because it would imply the presence of parts there. One
might think that it would be impossible to create the physics of motion under
such conditions. But this is not so, and there are ways to do this, as there
are real processes which can develop without triggering imbalance in the body
of their agent.
Our modern
notion of continuum is that of a continuous material environment whose properties
are constantly changing in space. Whereas a continuum which consists of no
parts never changes its properties in space. Which implies an entirely different
approach, different physics and different original basis. It would be useful to
know what processes and phenomena are lying hidden along this so far unexplored
path.
It would be
impossible to create either a proper world picture, or a good scientific school
unless a deep understanding of science, natural philosophy foundations and
primary problems is reached. And the foundation of science is based primarily
on a seemingly natural assertion: “The World Is! And it’s material.” It’s a
dogma, pure and simple, without accepting which one can forget about such
material science as physics. To prove the validity of this dogma, i.e. the
material nature of the World, one has to show the proto-element with which this
World is built. An impossible mission because beside matter there’s always
‘something’, that’s why in such cases the argument is substituted by sensual
beliefs, but in the majority of cases they use the notion of a ‘fact’.
But hasn’t the
modern science accumulated too many things which are taken for granted, with
attributes thought inherent? Let’s cite the notions and phenomena they derive
from which in physics have so far received no scientific interpretation at the
level of processes which form these phenomena: continuum, physical vacuum, ether,
the speed of light, space curvature, various fields, motion, inertia, mass,
force, gravitation, energy, electricity, invariance, elementary particles,
expansion of space, singularity.
It’s apparent
that the endlessly divisible continuum is infinite in depth, i.e. in theory
it’s impossible to get to its root-cause. Nor one would try to dispute the
infinity of the in-bound chain of the cause-and-effect relations which ensure
the physical phenomena, processes and properties we observe. Which implies that
any fact or inherent property is bound to have its root-cause. Motion, for
instance, or rather, the object’s transfer in space (in continuum). For the
body to move in continuum and relative to it, changes should emerge in the
processes which ensure this motion. And if the speed of motion has changes, the
processes have changed too. The reverse is also true: the changes in the nature
of processes trigger the change in speed. One should bear in mind too that the
absence of motion is also ensured by certain processes, and as the body and
continuum are in constant interaction (the body being a manifestation of
continuum) then any changes in the processes trigger the body reaction. But
what are these processes, and what is the essence of their mechanism? And what
if continuum is infinite and consists of no parts? What then? It’s not as if
such continuum might have disturbed unstable parts…
Rhythmus: What do you mean ‘the essence of their mechanism’?
Dynamicus: Each process has its mechanism. Say, the field affects
the body and makes it change the regime of movement. But what processes in the
continuum determine the existence of the field as a phenomenon? How do these
processes affect the body and in what way? How do these changes become
transformed into motion? In other words, what’s the mechanism? Any talk about
the force of the field being the actual cause of motion sounds more like ritual
chants rather than physics. The mechanism is a supposed or specific chain of
processes which ensure the phenomenon’s fact.
So, we’ve
accepted the dogma ‘The World Is, and it’s Material!’ To begin the
construction of a model of the universe (though the author sets a more modest
task of constructing a model of the phenomena in the universe), we need such
things as: container, continuum, the presence of processes, the observer. The
construction begins with the latter. The observer’s presence in the model is
crucial, first of all, so as not miss the impact factor of the observer
himself on the observed reality, and his perception of this reality.
Observer is the
pivotal point there. Without observer, continuum and the developments there
need no explanation, they exist as they are! Whereas the completeness of
explanation depends on the instruments used by the observer, among which are
the sense organs, the mind and technical devices extending the observer’s
abilities. The process of building a picture of the world passes through
numerous stages: the sense organs become stimulated by the incoming information
→
the stimuli
are transformed into signals entering the brain → the brain assesses the
incoming information, classifies it and presents it in a form suitable for
presentation → after which the question rises about the user and his
agent, i.e. some entity which directly receives this information.
We cannot fully describe the
observer, though he’s actually the focal point of all knowledge about the
surrounding reality.
As for this entity which plays the
role of the information user’s agent, which we might call the Soul and take
steps to find out what it actually is, we might run into another global problem
which the rabid materialists are careful to side-step, saying there’s no soul
because there’s no experimental proof of it. Whereas it’s precisely the soul,
and every man feels it, which receives and assesses information. The issue of
information ‘user’ is even more complex, besides it lies beyond the scope of
this book.
Seeing the
complexity of transformation of the input, coming from the outside, into the
inner image, now we cannot assert that the surrounding world is actually the
way we imagine it to be. In this sense our idea of the world and what’s going
on in it is always subjective because the real world may differ strongly from
our inner perception of it. A good point in question is a connection between
the type of information (the form of its presence) on the computer’s hard disk
and its outward presentation on the display: a nice picture on the display, and
entirely different thing on the hard disk. The information received from the
monitor in no way reflects its actual state on the hard disk. Which means that
we do not know what we are actually dealing with, and what it all amounts to.


Fig.1 The object’s outward appearance in jpg. format
(left), and a fragment of its computer presentation in the intermediary,
between the hardware and display, doc. format (right).
Undoubtedly, the
world we are studying does not match our notions of it. For example, the
rainbow has no colors but signals of varying frequency; it’s our brain which
colors these signals. For this reason lots of processes and phenomena natural
in the real world may seem to us strange and illogical, sometimes completely
beyond our grasp. This is also due to the fact that the researcher lacks
perceptual abilities allowing him to receive fully the data coming from the
surrounding reality. For the observer such information is latent: the processes
and phenomena do exist but there’s no way to perceive or register them. In this
sense the observer is always dealing with a limited notion of the object of his
studies. That’s why the physical models he creates are often incomplete, and
the yawning gaps emerging there are customarily filled with speculations in the
form of axioms and postulates. Alas, there’s no other way for us to judge about
the universe. And lots of things exist and take place beyond our range of observation.
Container and
continuum
Container and
continuum which fills it pertain to the category of undefinable. The only thing
we can do here is to philosophize, but we cannot penetrate into the physics and
the logic of such entities. In essence, we do not know what exactly we are
dealing with, but we feel that container and continuum do exist, though in a
transcending reality, and we therefore accept them as a fact. Besides, our
choice is always limited: either materialism, or idealism. Let’s present our
own view of container and continuum.
Container: endless and absolutely empty; related to nothing and existing
independently, possessing neither essence, nor content; logically
incomprehensible and thereby without physical description, i.e. without
rational explanation.
Role: to contain
something.
Property: always
filled.
If absolute
emptiness cannot exist by definition, and it’s not clear what the container is
filled with, they speak of continuum. Its essence, too, is beyond physical
description, or logical comprehension.
Continuum:
continuous, incessant, uninterrupted, indivisible, consisting of
nothing.
The logic of the
latter assertion is that if continuality were measured by endless divisibility,
such continuality would have no proto-element, nor could have it. And if the
dividable continuum has no proto-element, the question arises about the continuum’s
physical reality. Such paradox can only be solved through conditional agreement
in which continuum is recognized as really existing.
The main role
and the continuum’s feature: to be the proto-element of all.
Processes
We presume the
elements of matter are the result of the disturbed state of continuum, and we
know that this presumption is more artificial, than justified. Still, continuum
has always been and will remain the carrier of disturbance, even if these disturbances
are not linked with the ‘shiftsome’ nature of the carrier. (Later on we will
reveal the cause of the doubt which emerged and describe the state of
processes, real for the observer, in which the use of the disturbed continuum
is unnecessary).
Outer and
inner observers
One cannot
separate the observer from the observation of a phenomenon. His observations
are always subjective. The observer is always a part of continuum, and he’s always
inside it. He cannot be an onlooker and observe the world under study from the
outside. But he can create models in which he poses as an onlooker. So, the
observer acquires a chance not just to assess the proceedings being outside the
model he created, but to analyze them from the inside as if he were a part of
the proceedings examined in his model. The simultaneous look from the outside
and inside makes it possible to form a more comprehensive picture of subject
under study. The observer’s most useful quality is his ability to go outside
the limits of his model in which the phenomenon is examined, and assess the
proceedings from the outside.
After a deep
examination of the Elements one finds nothing which could justify their
recognition as the foundation for the creation of the physical picture of the
world. The observer’s idea of the elements is most likely to be based on
his deep-rooted spiritual essence. ‘Something’ inside prescribes, and we
therefore are obliged to accept such elements: being, on the one hand,
unable to imagine and suggest something different, on the other, because of our
deep certainty that we are right, it’s the only possible way, and there’s no
other!
Rhythmus: What a surprise! The fundamentals of physics are
nothing but our inner convictions? How about experiments, the ages-long
experience, the accuracy of mathematics? Don’t they count for anything? You
think the whole of physics, including the modern one, has no solid foundation?
Dynamicus:
The modern physics is the knowledge for those who do
not care for the root-cause: they have formulas; if they coincide with their
calculations, they are therefore correct, and they actually show what the world
is. Few are asking the question as to how come that the world seems real for
us? And is it really real? The more so that its foundations are based entirely
on speculations and sensual-experimental practice, beside which there simply
cannot be anything else.
Postulates
Postulate
(Latin: postulatum), a hypothesis (a claim, presumption, regulation)
advanced as an essential presupposition, condition, or premise of a train of
reasoning. The latter often serves as a justification for the hypothesis’
acceptance.
The modern
interpretation of postulate uses experimental fact as reasoning. The postulate
of inertia could be cited as example: inertia manifests itself almost always.
In physics,
experimentally discovered phenomena which have no explanation are often presented
as postulates. Properties are usually regarded as innate, and therefore require
no explanation. For example, the property of space to curve is a secondary
postulate explained by the innate property of mass to curve space. The mass
requires no explanation being experimentally proven fact, i.e. the initial
postulate.
Many researches
find any explanations of the innate properties through examination of processes
superfluous because the physics’ calculus requires no additional entities. The
modern physics in a way resembles a Lego set whose pieces are much like
postulates. If this ‘Lego’ physics lack some connecting element, they first
invent it then create a postulate-hypothesis of how this happened, like in the
case of neutrino or gravitation waves when they made up for the absent after
which intensive search was started for experimental proof.
Nonetheless, the
number of postulates in physics can be significantly reduced. How? Take Lego
for example, which presents every complex component through a number of small
universal elements in such a way that a set of these elements can be used to
assemble any complex component or structure. If earlier a score of complex
components played a role of independent postulates, after the introduction of
several types of the lesser sized basic elements the number of
components-postulates may be reduced drastically. But the emergence of new, so
far unknown, elements is natural too.
To implement
such reduction in physics one has to find something which the whole range of
phenomena has in common, something which is responsible for the establishment
of their characteristics. Thus we found that motion, inertia, mass, interactions
of forces, self-organization, size reduction during motion and energy flow are
explained from a single position, i.e. a single algorithm lies at the bottom of
these phenomena and properties. This algorithm is presented in the form of
familiar elementary phenomena and processes the combination of which produces
different properties: motion, inertia, mass, interactions of forces,
self-organization, size reduction during motion and energy flow.
Rhythmus: What’s this, another revolution? Curious. And at the
same time you are suggesting that the World in which we exist may not exist?!
So what’s the use of your dogma “The world simply is!”? Everyone knows this,
and there’s no need to prove it!
Dynamicus:
I cannot prove that the World really is. As for your
proof, it’s of the carrot and stick grade. Scientific methods cannot prove
anything in general. One can only accept this or that postulation on the nature
of research. Otherwise you can forget about matter, and about science too.
Back to contents ↑
§ 1.02. The choice of instruments
Galileo
introduced experiment in physics as a means of learning. At the time a
revolutionary step which made it possible to separate science from fiction and
elevate science to a new level of understanding of the essence of nature’s
manifestations.
Traditionally,
experiment has been regarded as the criterion of accuracy of a theory. But experiment
is only the final phase of the research, the end result; the rest are our
guesses, hypotheses about the processes which, in the observer’s opinion, ensure
the fact of what’s taking place. For example, if the body falls on the surface
of earth, its fall is described mathematically, and its cause is thought to be
gravitational field. The fall is the fact, whereas gravitational field, at
least initially, is an assumption.
Sure, the
accuracy of mathematical description is tested by experiment, but neither
mathematics, nor precise measurements of changing, during the fall, speed parameters
say anything about the cause of the fall, nor about the nature of the existing
force. Experiments only confirm the match of their mathematical description
with the fact. For example,
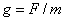 - where’s the cause
of the fall in this formula? If you say that the cause of the fall is force,
then what’s its origin and how does it make the body move in space? If you say
the space became curved, then say what curved, how and why? If you say we are
dealing with the innate property, then you are talking about the
incomprehensible reality, something which
physics is bent on mathematizing.
- where’s the cause
of the fall in this formula? If you say that the cause of the fall is force,
then what’s its origin and how does it make the body move in space? If you say
the space became curved, then say what curved, how and why? If you say we are
dealing with the innate property, then you are talking about the
incomprehensible reality, something which
physics is bent on mathematizing.
The ignorance of
the cause at the mechanism level is usually compensated by a hypothesis, which its
author, as well as his followers are trying to validate mathematically. If
arguments are strong enough, the hypothesis acquires a status of theory, in
other words, theory is the same good old hypothesis stacked high with
arguments. So, one has to be constantly aware that all our notions of the
universe are subjective. If we had different sense organs, our notion of the
world would be different too. Which means that any hypothesis is nothing but a
subjective view of the reality. That’s why one hypothesis is always replaced by
another.
Take gravitation
for example. It’s became a universal habit to explain gravitation by the presence of gravitational field and its innate
ability to affect the bodies present in it. This ability is called gravitation
force. But what sort of force is this? Does it really exist? Or will it be more
appropriate to say that gravitation force creates certain conditions in space
which make the body, once in them, change? May be, it’s some processes in the
body itself which make it self-propel toward the source of the field?
Such positioning
of questions focuses attention on the cause-and-effect chain: massive body →
the field of gradient conditions (gravitational field) → small body →
field-imposed changes in the small body → broken balance of the inner
forces in it → reaction to disbalance, attempts to restore balance →
accelerated self-propulsion as a means of balance restoration.
In that case one
should regard as the ultimate cause before the actual fall of a small body toward
the big one not the field itself but those changes which are taking place in
the small body, right? The logical chain built thereby allows us to conclude
that if the body is not affected by the field, it won’t react to it, i.e. it
won’t fall. With this link missing in the cause-and-effect chain you won’t see
the final result, the fall.
Hardly anyone
would deny the fact that ‘force is the essence of action, but not the action
itself’. For example, one can apply with equal vigor a magnet to the
bodies placed close together and made of dielectric and iron, but with
evidently different effect. Therefore question arises: what parameters and processes
has the magnetic field exactly changed in the iron body, and which it failed to
change in the dielectric one?
Limited by
stereotypes of thinking, few of us are aware that when the question arises
about the cause-and-effect explanation of fundamental things the proof is often
substituted by axioms and, literally speaking, ritual chanting. Here are examples: motion is an
innate property of the material world; inertia and mass are innate properties
of the material bodies; the speed of light is constant in inertial frames of
reference due to the accuracy of the invariant theory; the force of action is
equal to the force of counteraction; the physical vacuum which fills the space
is expanding and creates the effect of moving apart galaxies. To this they add:
“That’s how nature works”. And very few are trying to study the mechanism of
the very same motion, inertia, or invariant theory. Some researches sincerely
believe the mathematical descriptions they have of this or that phenomenon as
well as their correlation (mathematical, of course) with other phenomena are a
sufficient enough proof. Mathematical description of phenomena and processes is
not physics, but physics’ instrumentarium.
If opinion poll
were conducted among physicists about the root-cause of the inertia of the body
in motion the majority of them would maintain that the cause of the body’s
movement in space is a force applied to it which gave this body a certain
quantity of motion:
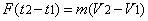 . (1.01)
. (1.01)
Formally,
correct. But the question was not about the cause of the beginning of body
motion, but about the inner and outer processes which ensured the transfer of
body after the force had been applied to it.
Many would
regard such way of putting the question absurd because classical mechanics
never examines any internal processes which ensure the fact of motion by
inertia: the body moves uniformly and rectilinearly if there is no external
force on it, or the net force on the body is zero. And the quantity of
motion, once received by the body from external force, cannot be the cause of
its subsequent motion because when moved to the reference frame of the moving
body its quantity of motion becomes zero. They usually refer here to the
invariant theory of Galileo and Newton’s relativity which prohibit to differentiate
parameters of two equal bodies if there’s no relative motion between them. Here
we encounter for the first time expression of pre-Einstein’s theory of
relativity imposing a tacit ban on the study of absolute differences and
recommending to examine only relative differences. Within the limits of the
classical mechanics it’s correct because they are founded implicitly on the
postulate of absolutely empty, filled with nothing container.
But no one has
yet managed to imagine the absolute void; the absolute void in the volumetric
container is beyond human imagination. Although the surrounding space seems to
us empty, there is a sufficient number of physical effects, like interference
and diffraction of light waves, indicating the presence of ‘something’ in this
space which possesses the property of transferring the waves. This ‘something’
is in essence more akin to the wave nature rather than the absolute void. This
is one of the reasons why in the early science they adopted the notion of
‘ether’: thin, imperceptible medium through which light is transmitted. Further
on we will avoid this notion because of the large number of speculative models
of ether: ether as a super-liquid quantum fluid; ether as a crystal; ether as
gas; ether as densely packed ideal balls, etc.
We do not know
what actually the luminiferous ether is; its only property that we know for
sure is the speed of light rays’ (electromagnetic waves) transmission which
equals 299792,5 km/sec. But even here we encounter a problem: how to establish
the speed of light in one direction. This problem was indicated as far back as
James C. Maxwell, in his famous work «A Treatise on Electricity and
Magnetism».
Albert A.
Michelson attempted to prove experimentally the existence of luminiferous
ether. In 1881 his famous experiment was conducted in which he failed to detect
the absolute motion of the Earth through ether. The scientific community was
plunged into a crisis: by the time the existence of ether was a foregone conclusion.
This crisis lasted for 24 years during which numerous attempts had been made to
explain the experiment’s negative result. At the time the scientists were
unable to understand the true cause of failure of Michelson’s experiment. In
1905 Albert Einstein published his paper "On the
Electrodynamics of Moving Bodies"
in which he suggested at the time
irrational but a unique way of explaining electromagnetic phenomena without the
use of ether. The scientific community worn out by the crisis gave a lukewarm reception
to the Einstein’s work which they regarded as interim until they discovered
this dodgy phenomenon which canceled the expected result of A. Michelson’s
experiment.
A hundred years
later, in 1981, such phenomenon, indeed, was discovered theoretically, and in
1990 was proved experimentally. But by the time the Einstein’s theory has
gained the status of the top leading paradigm. We are yet to return to this
issue because now we have a unique possibility of not just explaining the cause
of failure of the experiment which was to discover the absolute motion of the
Earth, but also of going back to the old, pre-1881, classic-ether positions so
as to continue the development of the scientific line which was first suspended
in 1905 and later completely rejected. Hence the task: creation of a universal
and conflict-free scientific instrument which anyone could use no matter what
scientific prejudices he might choose to stick to.
In science,
theory is such instrument. But the question always rises: Why do we need a new
theory? What’s the new instrument for? We’ve more than enough of them as it
is…”
To explain the
motives which emerge due to dissatisfaction with, say, classical mechanics I’ll
give several examples.
The classical
mechanics is employing the invariant and relativity theories – which has
certain advantages, but there are disadvantages too.
For example: Let object A and object B move in one
direction with speed
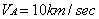 and
and
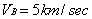 . Which of the objects, whose masses are equal, has greater quantity
of motion?
. Which of the objects, whose masses are equal, has greater quantity
of motion?
If the problem’s
condition had a reference frame in which and relative to which the objects’
speed parameters were to change, the solution would be simple:
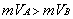
The problem’s
condition is incomplete, so the question has at least two correct answers:
1.
Relative to object À: 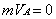 ,
,
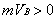
2.
Relative to object Â: 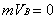 ,
,
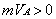
Another example,
showing the absurdity of the invariant theory.
The observer of
the reference frame with mass m pushes a reference frame with mass M,
with M >>m. The observer m notes that the force he exerts Fm
gave the object M a momentum MV.
He also finds that his actions brought speed V
not just to object
M
but to all visible objects in the universe. The
observer m concludes that object M has some rigid link with all objects
in the universe, and following the familiar formulas calculates the mass of the
universe: 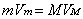 , with the speed of
the observer’s reference frame being zero (his reference frame the observer
regards as the main one), the mass of the universe is M=0.
, with the speed of
the observer’s reference frame being zero (his reference frame the observer
regards as the main one), the mass of the universe is M=0.
“Wait a minute”,
an opponent would argue, “in the process of exerting force it’s the observer m
who would feel more than M the inertia-born reaction to
acceleration. So it’s he, m, who’s changed the speed, not the object M”.
Ok, let’s accept
this. Suppose the reference frame m has changed the speed. But
relatively to what? Besides, the object M, too, has changed its speed
relatively to the same thing. What’s to be done? Should one refer to the
conservation of the center of mass? It’s relative as well… , only we cannot say
for sure relative to what? In this respect, the mechanics of Galileo-Newton in
its pure form is a theory of relativity!
Let’s examine
another curious situation. Suppose we have a sailing boat with an electric fan
firmly fixed in its stern (fig.2). The air from the electric fan flows in the
sail. With what speed V is the sailing boat to move? Will it move at
all? And if it moves, will its speed be relative?
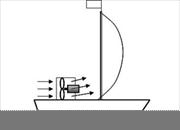

Fig.2. In some colleges students are asked to solve
the problem: “Is it possible to propel a sailing boat by aiming at its sails
the air flow from a powerful electric fan fixed in its stern?” The mediocrities
are offered a standard answer: “No, the boat won’t sail because the force of
pressure from the air flow is an internal force which cannot give a single
joint momentum to the boat and electric fan in it.”

Fig.3. The Fan Cart With Sail appliance showing the
relation and direction of the thrust force to the form of the sail. Source:
http://www.oberlin.edu
There was little
doubt that the sailing boat would move in the direction of the air flow produced
by the electric fan, i.e. forward. And that’s how it turned out to be. The
working model of such boat was made, and during its tests it reached the speed
of 3 km/h.
The author
invented and made this boat independently not just to demonstrate the
shortfalls of school education, but as a toy to amuse both children and adults.
But soon afterwards he found in the Internet an analogy, “Fan Cart with Sail”.
Let’s enumerate
the forces acting on the boat: the reaction of the electric fan to the air flow
it propels toward the sail; the reaction of the sail to the air flow from the
electric fan; the reaction of the sail to the incoming air-flow which emerges
as a result of the boat’s movement (the frontal resistance); the friction
between the boat and water.
The cited
factors split into two categories: those acting and counteracting. If action
and counteraction moduluses are equal, the boat sails with constant speed, and
in such cases they say that the force of action equals in modulus the force of counteraction. And if the opposite
forces are equal, what’s the mysterious cause of its movement, with the zero
net force on the boat?!
Guided by the
definition “Force is the essence of action, but not the action itself”,
one should raise the question: “What do the forces acting on the boat change
in the boat’s body? And how do they make it move with the zero net force?”
Are these changes real and pertain to the boat’s body, or they are of ‘relative’,
fictitious, nature? And if these changes are real, what are they? At what level
of matter organization do they take place and in relation to what?
Let’s take a
look inside matter, what changes take place there? The bodies moving and
resting in the continuum differ in parameters of the interacting elements. The
external macro-movements are formed and sustained by asynchronization of processes
at the micro-level. To understand this asynchronization one has to use some
instrument. Whereas we have neither the methodology of analysis, nor equipment,
nor any theory. The Rhythmodynamics suggests to use the wave geometry which
differs from the Euclidean one by the use of the foundation axiom.
Back to contents ↑
§ 1.03 Axiom of
foundation-regularity (introduction
of the carrier of constructs in geometry)
Although science
rests on its initial dogma ‘The world is! And it’s material!’, in its modern
form it has lost its secure foundation, the proto-substratum. Instead, it has
adopted other vague notions, like physical vacuum, independent field
formations, space-time continuum, relativity.
For example, the
‘physical vacuum’ literally means the absence of something, which at the same has
real physical properties. The time-space continuum curves, expands whenever it
suits mathematicians, while relativity implies absence of absolute foundation,
the basis. The main argument used there is ‘That’s the way nature is!’
But is it
possible for the real world to exist without the proto-foundation, which our
mind finds it convenient to consider as a carrier, environment? Many modern
researchers think this carrier notion is superfluous, i.e. they’ve found a way
to manage without it, replacing it with the void, fields (special kinds of
matter) and math.
Two planes
are flying parallel relative to air. The speed of one is 500 km./h., the speed
of another is 600 km./h. If we need to find only the relative speed, do we need
the speed of air relative to the planes? The air as the foundation for flying
is present, i.e. without it the flight itself would be impossible, but it can
be ignored in calculations. Nor does the speed relative to air has any impact
on passengers which doesn’t mean it’s absent. The relative speed of planes is
100 km./h., and if we ignore the air, there’s no need to find the speed
relative to it. Why increase entities without necessity? Of course, if the air
were bursting in the portholes, it would be entirely different matter…
Relativity is
present in Euclid’s geometry too. Because it has no carrier of constructs in
the axioms of foundation (the word geo-metry indicates the carrier of
constructs, but for some reason it was omitted from axioms). In practice such
carrier could be: the surface of the Earth, school-board, a list of paper,
computer display, etc. In geometry the carrier of constructs is always implied,
but its importance is usually overshadowed by the conditions of the problem to
be solved. If geometric constructs change in time, say, two dots move on the
list of paper, then try as geometrician might to justify his logic by
relativity, these dots, first of all, are moving relative to the material on
which the constructs are made, i.e. relative to the carrier of constructs.
It’s to this
carrier that the main reference frame should be tied to.
Let’s formulate
the foundation axiom which Euclid’s geometry lacks. We call this axiom
‘foundation’ because without it we’re unable to define or construct anything.
The
Foundation Axiom: There is foundation in the form of a carrier for
constructing (presenting) dots, direct lines, planes, circles, two and
three-dimensional figures. Dots, direct lines, circles, planes, two and
three-dimensional figures cannot be constructed without the carrier, even if
it’s an imaginary carrier.
Rhythmus:
But why do we need this carrier of constructs? We’ve
managed without it, haven’t we?
Dynamicus:
Somehow we have, and until 1905 we didn’t need it
much. May be, because we didn’t question its existence. By the way, physics still
uses oblique synonyms to carrier: space, physical vacuum. But sooner or
later, one has to define one’s position. If we recognize the carrier, then
everything takes place in it and relative to it; which brings clarity and
certainty. If the carrier is rejected, anarchy starts in physics where
each is free to invent his own foundations.
Back to contents ↑
§ 1.04 Wave geometry
In geometry the
carrier of constructs plays the role of the absolute frame of reference (AFR).
It’s necessary in order to use the Euclid’s geometry in modeling the wave
physical processes.
Without the
carrier the modeling of wave processes is impossible, or it is possible but
with additional opening conditions.
There are
several kinds of geometries:
·
Static geometry
with
fixed points, lines, figures and relations between them. The static geometry
has no notion of ‘time’.
·
Kinematic geometry
in which the points, lines, figures move, and relations between them
change, according to the set rules. Kinematic geometry is impossible without
the notion of ‘time’.
·
Wave geometry –
a
branch of kinematic geometry aimed at studying the periodic wave phenomena,
processes and relations between them. The wave geometry is based on the axiom
of the carrier of constructs, i.e. ‘wave medium’ All movements and transfers in
wave geometry take place in, or on, the carrier of constructs, and therefore
the parameters of those movements and transfers are measured in relation to the
carrier. The carrier of the constructs is constant, never changes its form
under any circumstances, i.e. serves only to display the movement of waves on
it, as well as the movement of points, direct lines and figures.
In nature the
role of wave carrier is played by the wave medium which transfers the wave disturbances
always with the constant velocity through itself and in relation to itself.
Having introduced the axiom of foundation, we thereby have brought the wave
geometry closer to the real physical mediums and waves. The difference is that
in wave geometry the carrier doesn’t become deformed under any circumstances,
whereas in reality, for example, on the surface of water, or in acoustics, the
waves are impossible without the deformation of the medium. As for the
electromagnetics, we have no idea what happens with the medium when electromagnetic
waves are transferred.
Rhythmus:
Here’s again an implied return to ether. Hasn’t
Michelson proved that it doesn’t exist, nor can exist. Or your special opinion
is just a reflection of nostalgia?
Dynamicus: This opinion is logically justified! The only way to
prove the absence of the wave medium called ‘ether’ is to measure the speed of
light in one direction. As long as there is no such experiment, there is no
proof of ether’s absence! And the necessity of such experiment was stressed as
far back as James Clark Maxwell. But the modern scientific clan driven by
business interests is terribly unenthusiastic about it. Therefore they possibly
either avoid any public experiments on this issue, or they may have done
something and keep the results secret. If this
is so, one can hardly call what they do ‘science’.
Let’s take an
example:
Suppose there’s
a dot (oscillator) on a two-dimensional carrier of constructs which emits periodic
waves in the form of circular fronts. Each point of the wave front is uniformly
departing from the source of transmission, with the velocity of the front being
tied to the carrier of constructs, not the source, which could be moving. A
system of departing wave fronts emerged around the source. If transmission
frequency is fixed and the source is stationary, the distance between the
fronts is the same, and it equals the wave length. An even and rectilinear movement
of the source (V<c) shifts the position of the departing wave fronts in
relation to each other. The fronts themselves remain always circular, with
their center being in the place of their transmission on the carrier. After
transmission the wave front is no longer tied to the moving source and other
fronts, i.e. exists on its own. (fig.4).
The classic rule
of adding velocities can be presented as
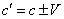 , (1.02)
, (1.02)
The Doppler’s
rule
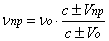 . (1.03)
. (1.03)
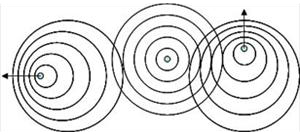
Fig.4 . That’s the way the processes in way geometry
look. The wave fronts spread in the medium with constant velocity. The speed of
their sources doesn’t affect the propagation of waves they transmit.
The absence of
carrier, i.e. wave medium, leads to ambiguity, particularly when the reference
frames are required to be invariant.
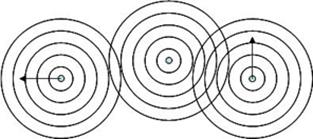
Fig.5. If one is to use the geometry without the
carrier one won’t be able to manage with one drawing only because each
oscillator, depending on the desires of geometrician, may be regarded as the
reference point. The absence of the carrier of constructs and the invariant
principle lead to ambiguity, i.e. inability to construct a definite
interference picture.
It’s interesting
that Euclid’s geometry is incompatible with Galileo’s invariant theory. It’s impossible
to construct a satisfactory interference pattern within the framework of absent
carrier and at the same tine the declared invariance of the sources. For
example: Suppose two equal in frequency sources are invariant. Suppose the
velocity of one of them is zero, the other – V. One has to construct the
changing in time interference of waves from the sources (fig.5). Obviously,
it’s impossible without breaking the condition of invariance, because the waves
are supposed to be circular due to the equality of the sources in relation to
each other. In this sense the Euclid’s geometry and invariance contradict each
other: even the simplest things cannot be constructed correctly because the
modern physics and Euclid’s geometry are incompatible.
The wave
geometry is the basis of rhythmodynamics. Its main postulates match the basics
of wave geometry.
|
Wave
geometry axioms |
Rhythmodynamics
postulates |
|
1.
The dot is the
oscillator, the source of spherical waves
2.
The waves spread in
the carrier of constructs and in relation to it with constant speed
3.
There can be any
number of dots-the sources of waves
|
1.
The oscillator of
infinitely small size, possessing no properties, except being the source of
periodic oscillations in the form of pulsations,
2.
Wave medium transforming
the oscillator pulsations into spreading spherical waves and ensuring their
constant speed of disturbance propagation in relation to itself.
3.
The emergence of any
other oscillator creates a system. |
The instrument
of wave geometry makes it possible to model processes and calculate the experiments’
results. That’s how it predicted (later this was proved experimentally) the
phenomena of standing wave compression, dependence of the speed of the system
of oscillators on the phase shift between them, dependence of acceleration of
the system of sources on the frequency difference, the speed of the energy
flow, the zero-amplitude way of energy existence, etc.
Back to contents ↑
§ 1.05 The properties of the wave geometry objects
As instrument,
the wave geometry allows to model the processes of self-organization of simple
and complex systems without any specific calculations of the interacting
forces. The modeling is based on the assessment of the state of medium around
the examined oscillator with the subsequent transfer of this oscillator toward
the area of the balance state. If this balance state area shifts, the
oscillator obediently follows in its wake. But the moving oscillator now emits,
due to the Doppler’s effect, the waves of a different length. These waves
propagate in the medium and bring changes in the state of the wave field. After
some time the waves which have changed their length reach the other oscillator
and change the state of its surrounding environment. Such change leads to a
transfer of the balance state area and, consequently, to the changed position
of the second oscillator: now it starts emitting in space the waves of changed
length. These changes reach the first oscillator and it reacts by motion. Such
process is repeated until the oscillators occupy stable positions in relation
to each other.
The oscillator
has no sense organs, and it knows nothing of any other, similar, oscillators.
What the oscillator can do is to interact with the environment and, detecting
any changes in its state, move in the direction of the area of its comfort.
The oscillators do have an impact on each other, not directly but through the
wave medium, through changes in its state. It’s these changes which make the
oscillator move, and it doesn’t care what caused them, how and why.
The most
convincing examples to this could be the experiments conducted by Carl Bjerknes
as well as by Ivanov and Didin.
Rhythmus: As far back as the middle of the 19th
century the Norwegian physicist Carl A. Bjerknes (1825-1903) proved that two
pulsating spheres, the radiuses of which are too small in comparison with the
distance between them, when placed in liquid (which cannot be compressed),
these spheres can trigger either mutual attraction or repulsion.
Dynamicus:
By the end of the last millennium Y. Ivanov and A.
Didin showed that two coherent sources of waves placed on the surface of water
can attract, repulse or create an elastic wave connection between each other
(form a system), as well as propel if the phase-frequency shift exists between
them.
One should
stress that in wave geometry the process of self-organization is witnessed by
only one outside spectator, and the process itself doesn’t need the
introduction of local, inner observers and the use of invariant principle the
way they do it now in physics. Naturally, the observation procedures can be
made more complex if we assign a local observer to each oscillator and remove
the outside spectator. In which case the conflict between the eye-witnesses is
inevitable because each of them has the right to regard his own oscillator as
the main reference frame. Which can lead to nothing but confusion. The lucid picture
which we could have is turned instead into
squabbles at mathematical level.
There is a
difference between the perception from the outside, and the perception taking
place inside. If we take this into account we’ll see why our assessment of
natural phenomena differs depending on our choice of the outer and inner
‘points of view’.

Fig.6. That’s how we see, for example, the ‘world’
from the outside (left), and that’s how – from the inside (right).
The semblance of
the wave geometry foundations and the postulates of rhythmodynamics makes it
possible to model the natural phenomena and observe the processes in their
ideal, undistorted geometrical version. In effect, the outside observer
acquires the ‘officially approved status’ which gives him the right not simply
to judge impartially the proceedings, but also at his own discretion to set
conditions and change parameters, and always stay outside the proceedings, i.e.
to observe things as they are.
Rhythmus:
Here we are: came back to what we’ve so painstakingly
avoided: the absolute observer, the absolute reference frame, wave medium. Too
many entities which we in the XX century worked so hard to get rid of.
Dynamicus: First of all, we are dealing with wave geometry in
which you cannot manage without the geometrician as outside observer. If it’s
more convenient for you to assess the developments from the inside, you are
free to do it. Only I think certain things are better visible from the outside.
For example, the difference between the depiction of the elephant made from the
inside and outside is obvious. And if you prefer the inside look, I’d rather be
outside. Both depictions are essential for the creation of a whole integrated
picture. As for the seemingly superfluous entities, try to cook pilaf without
water!
Back to contents ↑
§ 1.06 The wave geometry potentials
To assess
potentials of wave geometry (WG) let’s imagine a simple 2D model experiment:
two coherent oscillators at first stationary, then, with distance between them
unchanged, moving at a certain constant speed.

Fig.7. Phase shift is absent. V = 0 – no
transfer in the medium. Interference field emerged, as well as the standing
wave between the oscillators.

Fig.8. Phase shift is absent. Orientation to the
transfer in the medium is perpendicular (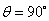 ). The speed of transfer V =0.75c. Direction
of transfer is from left to right. Interference field is compressed. Additional
anti-nodes and nodes areas have emerged . The distance between the standing
wave nodes has diminished.
). The speed of transfer V =0.75c. Direction
of transfer is from left to right. Interference field is compressed. Additional
anti-nodes and nodes areas have emerged . The distance between the standing
wave nodes has diminished.

Fig.9 Phase shift is absent. The system
moves to the right. The orientation angle toward the direction of movement
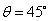 . The speed of movement
. The speed of movement
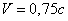 .
.

Fig.10. Phase shift is absent. Orientation
to the movement direction (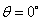 ) is parallel (oscillators move from left
to right). Motion speed
) is parallel (oscillators move from left
to right). Motion speed
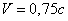 .
.
We can see without calculations that the interference pattern is
changing: it depends not only on the speed, but also on the orientation of the
oscillators’ system to the direction of motion. If the system’s speed and
orientation could vary, similar patterns might show that the higher is the
speed and the lesser is the angle of orientation, the closer the nodes and
anti-nodes become to each other. If we set as condition the numerical
preservation of nodes and anti-nodes between the oscillators, we would notice
the lessening of distance. We would watch the standing waves compress, and the
system’s size shrink. What’s notable is that these things were not calculated
mathematically, but modeled by rhythmodynamics.
Let’s examine another example: an interference pattern of a couple
of oscillators of different frequencies. This effect has received the name
‘spider-effect’ due to its resemblance to a spider.
Since moiré pictures first emerged the effect shown at fig.11
has repeatedly caught the eye of both ordinary people and serious researchers.
Still, no one happened to consider this interference effect
remarkable, and this beautiful effect failed to receive the status of important
physical phenomenon.


Fig.11. Spider effect.
And it’s the very same effect which emerges each time the waves from
the sources of different frequencies start interacting (interfering). This
phenomenon indicates concrete processes, including force and energy ones.
Another example: Non-radiant systems. Few persons know that
oscillators can be positioned in space in such a way that their net outwardly
directed radiation would be zero. Normally, they say in such situations that
all energy stays inside the system, but this opinion happens to be wrong. The
energy is radiated in the so-called ‘non-manifest’ form.

Fig.12. The system of coherent oscillators
on the plane. The outward wave radiation is practically absent. But this
radiation may become manifest at a certain distance away from the system, which
implies that unless you know about its source, the energy in wave medium will
be emerging as if from ‘nowhere’.

Fig.13
The case when the source emits in one direction two waves of equal
frequency, but each wave has its own velocity in the medium (such is the
medium’s property: it’s two-lane). The interference of such waves produces a
standing wave, i.e. stationary nodes and anti-nodes emerge in space. Inside
every anti-node, a transfer of energy takes place away from the source, what is
unclear is how the transferred energy behaves in the nodes. If we examine the
process within the limits of one standing wave, i.e. from one node to the
other, we would see that the energy emerges as if from nowhere (from vacuum, or
‘under-space’), travels some distance and disappears into nowhere.
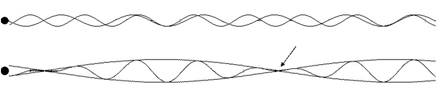
Fig.14
The other option is no less exciting. Suppose, we had two coherent
sources emitting energy in the form of rays in one direction, but at a very
small angle. In some area of space the rays intersect in the strictly opposite
phases and create a zone where they practically cancel out each other. Suppose
this zone is sufficiently large and the observer cannot register the overall amplitude
of radiations. The question: Is the energy present in this zone, and if so, in
what state?

Fig.15
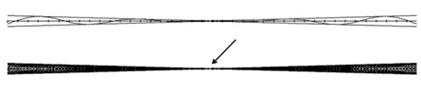
Fig.16 The arrow indicates a point where
the manifest energy is zero, while the non-manifest energy is maximal
Of course, the energy is present, and the state in which it exists
is called zero-amplitude. The zero-amplitude state of energy is noteworthy for
its effect: the energy travels in the medium (by means of the medium) while the
medium itself remains in a state of calm. Which means that the sources’ net
energy may be in both manifest and non-manifest states.
Energy and zero-amplitude way of existence
Let’s examine a model: Suppose we had two separate independent
coherent sources of monochromatic waves. The sources emit waves in one
direction along axis x. Naturally, in the areas where the waves
superimpose on each other their amplitudes may double or disappear. If the
distance between the sources triggers the wave’s phase displacement of 180° ,
then along the hole length of the axis x we are to observe the
disappearance of amplitude, i.e. the waves do exist, each of them carries
energy, but the energy is in such a state which makes it impossible for the
researcher and his instruments to register it. One might say there’s no
transfer of energy there at all. But this is not so. To prove the reality of
the energy transfer in the so-called zero-amplitude (non-manifest) state we
should conduct another mental experiment.
Suppose two monochromatic waves from two coherent sources travel as
rays in one direction at a very sharp angle (the minutest fraction of a second,
say, nought point ten or more zeroes…). The area in which the energy is
practically in a zero-amplitude state is large (the lesser is the angle, the
larger is the area); and if we, being inside the area, know nothing of the
experiment with the sources, our instruments would register no energy at all.
But farther away, in the area of space for us inaccessible, the rays began to
move apart. An observer in this area who also knows nothing of the experiment
would regard as a miracle the appearance of energy as if from nowhere.
And suppose this observer must give a credible explanation to this
‘miracle’ and create a valid theory of the energy’s strange appearance out of
the empty space. He can make such theory palatable only if he acknowledges the
empty space’s inherent ability to produce energy. As for us, we know the real
cause, and therefore we’ll have a different theory.
Rhythmus: I know what you are driving at. Now every
mad inventor would have a chance to explain the unbelievable energy efficiency
of his mechanisms by their ability to transform energy from its zero-amplitude
state to amplitude state, i.e. to drag it out of zero, the vacuum.
Dynamicus:
I used this example just to explain the
meaning of zero-amplitude. I hope the hypothesis of the presence in space of
real energy in its zero-amplitude state has received some rationalization. I
think the presented explanation hides the key to obtaining any amount of energy
anywhere in space. One only has to learn to transform it from its
zero-amplitude state into amplitude one. To understand it we now have a model
of the proceedings.
So, there’s no miracle there. If two rays intersect at a small angle
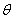 , there will be no complete cancellation:
, there will be no complete cancellation:
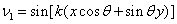 (1.04)
(1.04)
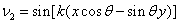 (1.05)
(1.05)
the result after subtraction
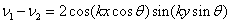 (1.06)
(1.06)
Complete zeroing
is possible only if the angle between the rays
 .
That’s why in the area of intersecting rays the wave doesn’t drop to complete
zero! This is quite evident from the drawing. But neither the formulas nor the
drawing can show in what strange state the energy near the zeroing area is and
how it manages, having passed this area, to completely restore itself.
.
That’s why in the area of intersecting rays the wave doesn’t drop to complete
zero! This is quite evident from the drawing. But neither the formulas nor the
drawing can show in what strange state the energy near the zeroing area is and
how it manages, having passed this area, to completely restore itself.
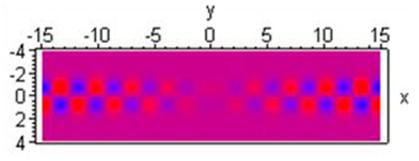
Fig.17
The interest to the non-manifest state of energy propagated by waves
has emerged in connection with attempts made to understand the root-cause of
continuum. If continuum is attributed with such properties as continuity,
indivisibility and unbrokenness it turns into a complete mystery how on earth
it can by itself transfer from one place in space to the other any disturbances?
Bearing in mind that any shift of one part of continuum’s body in relation to
the other would imply its divisibility and brokenness?!
To overcome the predicament one might use a trick well-tested in
science and say “That’s how nature is, and there’s nothing to do about it!”
Quite often they resort to it.
Indeed, why should continuum change its state in order to transmit
energy from one place in space to the other? This energy could well pass
through (along) the body of continuum in the so-called zero-amplitude state
while continuum would feel no need of relative shifts of its own parts. In this
case the Eleatic school concept of continuum is quite justified.
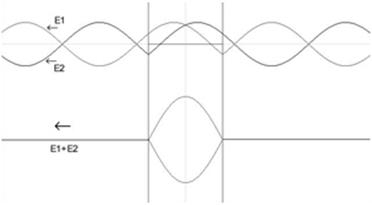
Fig.18. Illustration of the issue of
zero-amplitude state of energy.
It’s really difficult to imagine the zero-amplitude situation,
likewise it’s difficult to answer the question about the state of energy propagated
in real medium by waves in opposite phase. But now we at least understand that
such quite real processes can be unobservable. In other words, the energy
propagated by waves in real medium can be in two states: manifest (amplitude)
one, and non-manifest. Formally, the situation can be described as:
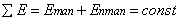 (1.07)
(1.07)
This formula expands the understanding of the law of conservation of
energy, i.e. it indicates that energy can be in any of the described states.
Rhythmus:
With your non-manifest energy beyond any
observation, for a researcher your equation would look like a violation of the
law of conservation of energy. Naturally, having introduced such instrument in
theory one can readily promise power stations producing energy out of ‘vacuum’.
Dynamicus:
Yes, this is quite likely, and such
generous and premature promises should be better tackled by the Commission on
fighting pseudoscience.
The issue of transformation of non-manifest energy into manifest
seems quite intriguing. It’s obvious that the non-manifest state of energy can
be easily characterized by frequency. Which means that in space at the same
time there can be non-manifest energies of different frequency. To obtain a
manifest energy it would be sufficient to skillfully transform the
non-manifest energy of one frequency to the non-manifest state of a lower
frequency. Formally, it would look like:
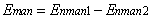 , (1.08)
, (1.08)
i.e. a certain appliance, let’s call it a frequency transformer,
seizes the non-manifest energy of high frequency and transforms it into the
non-manifest low-frequency state. During which the energy difference could move
into the manifest state.
Rhythmus:
I guess I’d have to read Tesla once again
on the issue of harvesting energy. Saying that “One has only to learn to
transfer it from zero-amplitude to amplitude state” you apparently intend to
make some appliance which could transmit energy from any space to the energy
reservoir which could later be used as a source of electricity?
Dynamicus:
The issue of transformation of energy from
one state to the other is not so simple and requires additional clarification,
laboratory experiments and demand on the part of society. As for the
zero-amplitude transmission of energy from point A to point B it
could be possible. As for harvesting energy directly from space, well, within
the framework of the drafted model such space must be crammed with energy in
zero-amplitude state at least because each radiating element of matter
(provided this element represents a system of lesser radiating elements) acts
as a kind of generator of such energy. Formally, nothing happens: ‘zero’ came –
‘zero’ went. In practice, a new sun comes to life.
The question of real state of processes which are registered by our
sense organs and instruments poses quite a problem here. It’s quite possible
that the world we are observing, our world with all its attributes is situated
at one of the non-manifest levels of processes’ organization in continuum. Such
levels could be numerous, and if we introduce an imaginary axis of coordinates
to mark those imaginary zero-amplitude worlds, we will have another, strange as
it is, dimension ( ).
).
Suppose our world were zero-amplitude one. But being inside it, we
observe its amplitudes, i.e. its materialness; besides we have an opportunity
to transform this or that energy process to a much deeper level of
zero-amplitudeness.
Having accepted our world as the usual one among the zero-amplitude
worlds, we are obliged to presume a possibility of ‘material-energy’ life in
the worlds similar to ours. This picture of the world could explain a lot, say,
where the elementary particles get the energy for their ‘recharge’ from –
still, for science it’s nothing but a hypothesis which could be seriously exploited
only in philosophy, esoterica or science fiction.
Of course, this hypothesis is a way below a theory status, but it
has one unquestionable advantage: it makes possible to understand how the
phenomena and processes which we consider real can happen without causing
disturbances in its own carrier, the proto-basis, substratum. In this sense we
have found a superconductor for processes.
One has also to admit that we have no prior experience in describing
physical processes and phenomena within the zero-amplitude notions. Nor there
any calculus for this.
Interference in supersonic regime is
another little-known phenomenon. It’s difficult to imagine a situation in which
the interference pattern moves in the wave medium faster than the waves in this
medium do.


Fig.19 In a supersonic cone of a single
oscillator a standing, relative to the source, field of wave energy emerges.
The velocity of this field equals precisely the velocity of the source (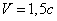 ), i.e. the field moves with the source. A picture
made from space shows a running wave pattern in the boat’s wake.
), i.e. the field moves with the source. A picture
made from space shows a running wave pattern in the boat’s wake.

Fig.20. That’s how the field of
distribution of wave (interference) energy looks produced by two supersonic coherent
oscillators. The velocity and direction of the field movement equal precisely
the velocity and direction of the oscillators
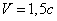 . The start of ‘Proton’ rocket. The energy
nodes and anti-nodes are clearly visible in the supersonic jet stream.
. The start of ‘Proton’ rocket. The energy
nodes and anti-nodes are clearly visible in the supersonic jet stream.



Fig.20.a Distribution of wave energy from
numerous sources (left model) moving at a supersonic speed (12 Max). Similar
process also takes place in the supersonic jet streams.
Many scholars know that the existing calculuses cannot fully
integrate those things which in wave geometry, and in nature even more so,
occur easily and unobtrusively. For example, the self-organization of wave
objects numbering over three. Such calculus requires a different approach,
a different logic. The first such program already exists, but it’s still far
from perfection.

Fig.21 a. Random initial arrangement of
coherent oscillators on display.

Fig.21.b A short time later the oscillators
created joint anti-nodes of the standing wave and became self-organized around
it, forming a circle.

Fig.21 c Gradually the circular formation
split into two lesser systems.
The potential of the wave geometry is not limited to this only. But
even this is already something!
Back to contents ↑
§ 1.07 Rhythmodynamics: postulates
Postulates in modern physics
Many researchers still think experience is the only source and
criterion of truth. If so, the foundation of the modern physical paradigm must
rest on phenomena and properties which are amply proven and therefore thought
fundamental. But if these phenomena and properties are not explained at the
level of processes, i.e. there’s no idea what processes exactly generate these
or those properties, then their proper place is among the phenomena of nature.
Note: One of the meanings of the word
Phenomenon (Greek phainomenon – to appear) is a rare or significant fact or
event.
Among the natural phenomena are: motion (there’s no explanation why
bodies can freely move in space); inertia (no explanation has been given yet
why bodies resist the impact); ability to interact (like gravitation, for
instance, the cause of which hasn’t been amply determined although this issue
was raised more then three centuries ago).
In other words, the phenomena and properties which lie at the
foundation of the modern physical paradigm, although experimentally fully
proved, can still be regarded as postulates because of the lack of
understanding of their physical nature. Objections may be voiced to this but
such objections could be justified only if the opponent were prepared to
present a concrete model of formation of at least one of the cited properties
and phenomena.
Rhythmodynamics’ postulates
Rhythmodynamics presents concrete means of illustrating natural
phenomena through their geometric modeling in the form of wave processes.
That’s what the ‘Wave Geometry’ has been created for: to discover and
clarify a range of wave phenomena which form the mechanism of motion, inertia,
interrelation ,etc.
One of the main criteria of any theory is the ability to predict
certain events and phenomena which could be later verified in practice. The
efficiency of wave geometry has been confirmed experimentally, when results
proved to match predictions. Among such instances are: the experiment to
determine compression of standing waves in acoustics; experiment to determine
the dependence of the speed of motion of the oscillating system of sources on
phase displacement between those source, and others.
Rhythmodynamics is based on the system of postulates:
1.
A hypothetical elementary object – a dot-size
mass-free oscillator which possesses the property of vibration (or pulsation),
exciting its environment and generating periodic waves in it.
2.
Medium which transforms oscillator vibrations
into parting spherical waves, ensuring their constant velocity of disturbance
transmission relative to the stationary source (in relation to the reference
frame, firmly fixed to the medium).
3.
Interaction, i.e. when at least yet another one
oscillator emerges, a system of oscillators emerges.
Explanation of the choice of postulates:
·
The mass-free oscillator, in case of an outside
impact, can without any inertia impediment pick up the speed of its motion in
relation to medium. Inertia properties spring up among oscillating systems as a
whole, but they are not attributed to single oscillators. We do not consider
the properties of a single oscillator because in such case they would require explanations.
Whereas a system of interacting oscillators develop a property of resistance,
say, to a change in its velocity. If the property, absent before, appears with
the system, it is attributed to the system, not to the elements of which it consists.
·
Medium is introduced without indicating its
structure and organization. The dependence of amplitude on distance is not
stated. One can even say the dependence of amplitude on distance is a property
of oscillating system, not of isolated oscillators.
·
The emergence of a system makes it possible to
speak of a stable form of its existence, as well as about localization of
energy in a specific area of space. The system allows to distinguish the
oscillators’ parameters (frequency difference, phase relations). Inertia is
first discovered at the system level (such property is inherently absent in
isolated oscillators) because of the finite speed of wave propagation (delay
effect) between the elements of the self-organized system.
·
To build a potent geometry-physical model a
number of auxiliary conditions are necessary. For example, each oscillator in
the system is seeking to occupy the most suitable to it ‘energy-comfort’ area,
a zone of durable balance, a potential hole and to always follow in its wake.
·
The presence of inertia in the case of isolated
elements (wave sources) indicates their complex structure, i.e. the presence of
a system consisting of component parts.
Back to contents ↑
§ 1.08 Establishing the tasks to be solved
Although the
number of issues Rhythmodynamics is focused to solve is limited, they are of
fundamental nature:
·
Dependence of standing waves parameters on the
motion of sources in wave medium.
·
Energy flow and its dependence on frequency
difference.
·
Interaction of wave sources. The basics of
self-organization of systems.
·
Phase difference and its impact on the speed
regime of propagation in the medium.
·
The cause of reaction to the external change of
motion regime.
·
Propagation in the medium triggered by internal
forces of propulsion.
Back to contents ↑
Chapter 2. Interference
Things are not the way they seem to be…
§ 2.01 Is it possible to manage without the notion of
wave medium?
It’s hard not to
notice the fact that by the end of the XX century a curious situation emerged
in science: matter has disappeared being substituted by equations. Long before
it, the existence of such trend had been pointed out by Vladimir Lenin in one
of his philosophical works but no one seems to have taken much notice. Now the
modern scientists who regard themselves as materialists fancy an
experimental-phenomenological cocktail in which physics is completely
substituted by math and absolutely weird models. The supremacy of this type of
fundamental physics lasted throughout the XX century and still continues.
Despite the
acknowledgement of the wave nature of matter, of light, radio waves, the scholarly
ideologists are still denying the existence of wave medium. A remarkable
paradox: there are waves, but there’s no wave medium! Such unwillingness to
consider the obvious leads to fragmentation of scientific outlook and,
correspondingly, to inability to create a whole and full working model. To
cover up one’s own intellectual disability one has to resort to such ‘potent’
explanations as “That’s the way nature is!” borrowed from Philistine arsenal of
wisdom called “All live like that!” or resort to intellectual speculations of
the type of: ‘fields as special forms of matter’, ‘mass as inherent property’,
‘curvature of space-time’ and so on and so forth. All of them emphatically
assert, none of then rationally explains.
As for the
author and his rhythmodynamics model, here the wave medium not simply exists,
it’s inseparable from the wave phenomena: without the notion of wave medium the
model won’t be able to work, and implement its universal function.
Back to contents ↑
§ 2.02 Standing wave. The basic properties we
know as well as new ones.
Standing waves
are ubiquitous. The reason is the bodies’ ability to reflect. In other words,
wherever you have waves and their reflection, standing waves are bound to
emerge. Hydro-waves, acoustic waves, light (electromagnetic) waves being
reflected by the surface are bound to create standing waves near it. Standing
waves are widely used in radio, electrical technology and metrology (to create
a standard of length, for example). Many chemists and crystallographers
especially have already come to conclusion that the bodies themselves are the
packages of standing waves, a kind of wave lattices in whose nodes atoms and
molecules reside. The standing waves can play the role of a primary structure,
and not just that. That’s why we attribute so much importance to this natural
phenomenon.
Let’s sum up
what we know about standing waves:
·
Standing wave emerges as a result of
superimposition of two waves moving in opposite directions and meeting the following
requirements: their wave frequencies are equal, their amplitudes are the equal
functions of the coordinate system. Standing wave is one of the manifestations
of the wave interference.
·
Standing wave emerges, for example, when the
falling and reflected waves superimpose, when the angle of incidence is zero,
and reflection factor is 1.
·
The amplitude of standing wave is a periodic
function of the x coordinate and doesn’t depend on time.
·
The point in space where the net amplitude is
always zero is called standing wave node. The areas between the nodes where the
net amplitude is above zero are called the anti-nodes of the standing wave.
·
The standing wave’s length is a distance between
the two neighboring nodes or between the two neighboring anti-nodes.
·
Unlike longitudinal wave, standing wave
propagates no energy. This is evident from a fact that the position of nodes
and anti-nodes in space doesn’t change in time – that’s why such waves are
called ‘standing’. The absence of the energy propagation by the standing wave
is due to the fact that the coming wave and its counter-wave carry energy in
equal amount but in opposite directions.
·
Standing spherical wave emerges as a result of a
superimposition of two harmonic spherical waves traveling in opposite
directions.
The simplest
case of emerging standing wave is the experiment with a string one end of which
is firmly fixed to a solid wall, the other is attached to an appliance
performing vibratory movements. If the latter end of the string is moved
continuously and made to perform harmonic vibrations, a sinusoidal wave is to
run along the string. When it reaches the point where the string is fixed to
the wall, the wave will bounce back and run in the opposite direction. The
superimposition of those two waves produces a standing wave in the string
(fig.22).
Fig.22
Now let’s talk
about the standing wave properties discovered by rhythmodynamics.
Let’s complicate
the experiment and replace the string with a thin elastic rubber tube (a hose).
To make it clearer, let’s examine fig.23 and describe the appliance with the
help of which we are to study one of the most unusual properties of the
standing waves.
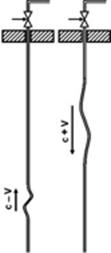
a b
Fig. 23 a) The rubber tube is filled with water, the
tap is closed. The velocities of the wave and counter-wave are equal.
b) The tap is open. The velocity of the water flowing in the tube is V.
The velocities of the wave and counter-wave are different. While in (a) case
one can expect the emergence of a standing wave of the type shown at fig.22,
in (b) case such prospects are not clear because it’s the waves of different
length which are to interfere! c) Counter-waves (left) produce the beat (right)
in which one can hardly make out a standing wave (Fig. 24).
One end of the rubber
tube passes through a hole in the wall and comes out on the other side. This
end of the tube is attached to a tap, which in open position lets water in the
tube. Some distance from its free end the tube is fixed to the vibrator
appliance, while the free end is inserted into a reservoir for water drainage.
Let’s fill the
tube with water, close the tap as well as the exit opening so that during experiment
the water could stay inside the tube. Moving, the same way as with the string
experiment, the free end of the tube with water we are to obtain the striking
and counter-waves of equal length, the superimposition of which is to produce a
standing wave.
Let’s change the
experiment’s conditions. Let’s open the tap outside the wall so that water
could flow in the tube with certain speed V. In the process of, say, a
single vibration of the free end of the tube we are to find that the wave
running to the wall is slowing down, while the speed of the same wave which
bounced back from the wall actually increased. Then, if the free end of the
tube is performing harmonic vibrations, we are to observe the superimposition
of two waves which have the same frequencies but different velocities of
propagation in the medium, and consequently, different lengths. This is
explained by the fact that the speed of propagation of the waves of deformation
in the tube with water depends on the speed and direction of movement of the
water in the tube. The speed of the waves along the water flow is (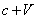 ), while the speed against the flow is (
), while the speed against the flow is ( ). Then, if the wave frequencies are equal, is the standing wave to
emerge? Or interference is to produce something which has nothing to do with
the standing wave?
). Then, if the wave frequencies are equal, is the standing wave to
emerge? Or interference is to produce something which has nothing to do with
the standing wave?
At first glance,
a beat should emerge which has nothing to do with the standing wave. The beat
does emerge (fig.24), but the standing wave also takes place. It won’t be
difficult to witness it either by solving the standing wave equation or through
computer processes’ modeling, or by staging the experiment itself.
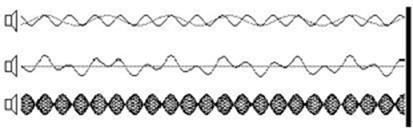
Fig.24 That’s how a computer model looks in which the
oscillations’ source is presented as a speaker. The direct and counter-waves
have equal frequencies but different velocities, and therefore different
lengths. Addition of these waves results in the beat. If this process is examined
as summed up in time, the nodes and anti-nodes will be visible which allows one
to speak of a standing wave.
Solving the
equation or modeling, we inevitably encounter the dependency of the standing
wave length on velocity V (2.02). This dependency differs from the
previously known (2.01), and here we for the first time encounter the ‘magic’
factor in physics (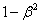 ). Such is the geometry
of standing waves in which 2.01 is a special case of 2.02. The phenomenon discovered
by rhythmodynamics was called ‘compression of standing waves’ (CSW).
). Such is the geometry
of standing waves in which 2.01 is a special case of 2.02. The phenomenon discovered
by rhythmodynamics was called ‘compression of standing waves’ (CSW).
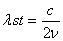 (2.01)
(2.01)
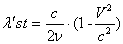 (2.02)
(2.02)
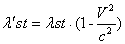 (2.03)
(2.03)
But standing
waves emerge in all wave mediums (electromagnetic wave medium is no exception).
Standing waves have long been used in electromechanics, radio engineering,
physics and metrology when, for example, the standard of length is determined.
That’s why the CSW phenomenon is paid so much attention in rhythmodynamics.
It’s worth note
that the compression of standing waves was first discovered in geometrical
constructs in 1981 (the author conducted geometrical analysis of the wave
phenomena related to Michelson’s experiment), then validated mathematically.
Only nine years later, in 1990, an acoustic experiment was staged which
confirmed this discovery.
Let’s dwell on
this experiment more because in its course I discovered compression of standing
waves not only with the lengthwise orientation of equipment, but with any
orientation. In other words, the experiment fully confirmed theoretical forecasts.
Before we start
describing the experiment, let’s ask a seemingly simple question: what is the
nature of acoustic waves? There are at least two answers:
1.
Sound is a mechanical (displacement) disturbance
propagated in elastic medium.
2.
Acoustic wave is a displacement interaction of
molecules by means of their own electromagnetic fields, i.e. the nature of
acoustic waves is electromagnetic.
I’ll describe
the 1990 experiment so that everyone who wishes could repeat it. The goal of
the experiment was to confirm the effect of the motion of medium or relative to
medium on the metric parameters of standing waves.
The plan of the
acoustic experiment (fig.25) doesn’t differ much from the experiment conducted
by Heinrich Hertz when he first obtained the electromagnetic standing wave.
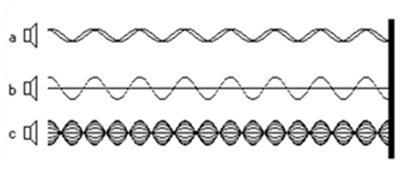
Fig.25 a) direct and counter waves; b) wave
superimposition: instantaneous show of resultant; c)
developing in time the resultant outlines in space a picture with well-defined
anti-nodes and nodes, i.e. the standing wave.
Fig.26 Hertz’ resonator
To create a
standing wave in sound medium one has to have a source of harmonic oscillations
and a reflector (acoustic mirror). As a source, one can use a speaker which
receives via an amplifier the signals from a generator. The speaker sends
oscillations in acoustic medium in the form of displacement disturbances which
the medium propagates in space through its own self in the form of waves. The
velocity of waves’ propagation is determined by the medium properties, like
elasticity, for instance. In the air such velocity varies, but at the earth’s
surface it amounts approximately to 330 m/sec.
Spreading in the
medium, the waves from the speaker hit the acoustic mirror, and bouncing off
move backwards. The superimposition of two opposite waves between the source
and the mirror results in a standing wave. This is in the ideal case when the
waves’ amplitude is constant and doesn’t depend on the distance from the
source. But in practice the amplitude decreases with distance which creates
certain problems of purely technical nature.

Fig.27. The map of the area where the experiment was
conducted (Russia’s western-most Kaliningrad region, the town of Luzhki. A view from space).
Fig.27 shows the
area where the experiment was conducted and position of the main pieces of
equipment (the source and mirror simulator) which helped realize the standing
wave. The distance between the source and the mirror was 70 meters. Which means
that the acoustic wave traveling back and forth covered 140 meters. The control
node, the one the changes in position of which were registered, was near the
source, therefore it was necessary to ensure in the node area that the amplitudes
of the going and coming waves be equal. This problem was solved by the method
of multiplication and division of frequencies.
Fig.28 Unit 1 consists of the sound generator,
frequency multiplier, mixer, amplifier and speaker. Unit 2 consists of a
microphone, frequency divider , signal restorer and low frequency (sound)
amplifier and a speaker. The ruler was used to register position of the control
node.
The driving
generator was tuned to frequency 3.3 kHz. This signal went simultaneously to
the amplifier and the multiplier, which increased its frequency four-fold (13.2
kHz). Two amplifiers and two emitters were used as a source. One of the emitters
was low frequency, the other – high frequency. The power of the low frequency
emitter wasn’t big, while the power of the high-frequency one was set so that
its signal could be received by the microphone placed on the acoustic mirror.
The
high-frequency signal received by the acoustic mirror was divided by four so as
to restore the low-frequency component of the radiation. After its restoration
the low-frequency signal was amplified and ‘re-emitted’ back to the source. The
amplifier capacity was adjusted so that the amplitude of the incoming signal
should be equal to the amplitude of the outgoing signal.


Fig.29 Pictures of the driving generator (a), and
mirror simulator (b) as well as phonendoscope (c) where 1 – is a thin copper
tube to search for the standing wave node.
These
manipulations made it possible to register the standing wave nodes in close
proximity to the source. The nodes’ position was determined with the help of an
updated phonendoscope in which the capsule with membrane was replaced by a thin
copper tube. The loose end of the tube was put in the standing wave, and by
moving the tube one could find the spot in space where sound was absent. This
spot corresponded to where the standing wave’s node was positioned in space.
The emitter and
the acoustic mirror were always set at a fixed distance mounted on wooden
marked with scales pillars dug into earth. To register position of the control
node of the standing wave a wooden ruler was used on which marks were made by a
pencil. The node’s position was determined manually with the help of the
phonendoscope.
It must be
stressed that had it not been for the acoustic mirror it would have been
problematic to discover the compression of the package of standing waves,
particularly with the wind directed along the appliance’s axis. Initially it
was planned to set up two opposite emitters, coherent ones and therefore
powered from a single sound generator. But analysis showed that emergence of
wind would shift interference pattern so strongly that it would have been impossible
to measure the expected result. So the solution was found in using the acoustic
mirror which completely removed the ‘noxious’ shift of interference pattern.
During the
experiment’s preparatory period calm windless weather set in (for three summer
days). This gave a convincing chance to witness that at every installation of
equipment with permanently adjusted parameters the control node was always
registered on the ruler in one and the same spot. So the only thing left for us
was to wait for the wind to appear.

Fig.30 Vane (left) Anemometer of revolving cups type
(right).
A self-made vane
was used to determine the direction of wind. An instrument measuring the wind
speed (anemometer) was not installed due to its absence.
Two situations
were of special interest: when the wind was blowing along the axis ‘source-mirror”,
and perpendicular to it. According to the calculations made, the standing waves
compression had to take place in both cases. To ascertain the fact of
compression of the package of standing waves one had to register the shift of
the control node toward the acoustic mirror. Below is the table of calculated
relationship between the wind velocity, reduction of distance between the nodes
of one standing wave and the shift of control node.
|
Wind velocity (km/h, m/sec) (along,
across) |
Calculated distance between the nodes (cm).
ñ=330m/señ,
í
=3,3êHz |
Calculated shift of control node (cm) L–L’.
L=70m. (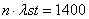 pieces) pieces) |
|
0,0km/h.
0,00m/señ |
5,00ñm |
0,00ñm |
|
5,0km/h.
1,39m/señ |
4,99991
|
6999,87
0,13 |
|
10km/h.
2,78m/señ |
4,99965
|
6999,51
0,49 |
|
15km/h.
4,17m/señ |
4,99920
|
6998,88
1,12 |
|
20km/h.
5,56m/señ |
4,99858
|
6998,01
1,99 |
|
25km/h.
6,94m/señ |
4,99779
|
6996,91
3,09 |
|
30km/h.
8,33m/señ |
4,99681
|
6995,53
4,47 |
The best weather
conditions for the planned experiment could be a pre-thunderstorm period which
has a spell of quiet after which emerges the wind which gradually changes its
direction. In the course of the following week such conditions emerged twice,
and both were used for measurements. After processing the obtained results an
unequivocal conclusion was made: whenever the wind emerged, no matter in what
direction, the control node of the standing wave was always shifting toward the
mirror – which testified to dependence in acoustics of the length of the
standing wave in the system on its, the system’s, speed in the wave medium.
Thereby the phenomenon predicted theoretically in 1981 was confirmed
experimentally in 1990!
Here’s another
experiment which could be staged in any ordinary school laboratory, or even at
home. (fig. 31). It requires: sound generator, amplifier of 1 watt, a speaker,
oscillograph, piezoelectric transducer and sufficiently powerful electric fan.

a) b)
Fig.31. Emergence of an air-flow between the speaker
and the wall (the air-flow is created by the electric fan) triggers deformation
of interference pattern and a shift of the control node toward the wall. The
package of standing waves is compressed.
Experiment
procedures’ order:
1.
Have series connected sound generator, power
amplifier and the speaker.
2.
Have sound generator frequency adjusted to, say,
3 kHz.
3.
Have the speaker firmly fixed at a distance of
2-2.5 meters from the concrete wall.
4.
After the speaker is switched on, make sure a
standing wave has emerged between the speaker and the wall.
5.
Piezoelectric transducer is switched to the
oscillograph. The transducer is used to determine the area of silence which
corresponds to the standing wave’s nodes. The oscillograph would show the
area of silence as a minimal surge of the running dot.
6.
After the node closest to the speaker is found
by the transducer, the transducer is fixed in this spot.
7.
The amplitude of the running dot is marked on the oscillograph.
8.
The electric fan is set 1.5-2 meters from the
shortest possible line between the speaker and the wall, aimed at it and
switched on.
9.
After the electric fan is switched on the
oscillograph’s readings increase.
10.
By moving the transducer carefully from the speaker to the wall a
new position of the shifted node is found (due to the insignificance of the
effect the transducer’s shift should be carried out with the help of a
micrometric screw).
11.
The node’s shift toward the wall shows that the air-flow from the
electric fan has changed the metric parameters of the standing wave.
12.
Conclusion: compression of standing waves’ has taken place!
The discovery
of this effect has an impact on lots of other important things, for example,
the issue of establishing a fundamental standard of length. If, using
interference method, a standard of length were created consisting exclusively
of a set number of standing electromagnetic waves and this standard were
compared with the platinum-iridium standard in Paris, an interesting picture
would emerge: the matter behaves exactly the way the artificially created
electromagnetic standing waves do. The root-cause lies in the matter’s
structure, in its wave nature, the wave nature of ties existing between the
matter’s elements.
Back to contents ↑
§ 2.03 Oscillations, standing waves, and
physical standards of measure
Oscillations
(pulsations) are one of the basic forms of motion. Any oscillation exists on
its own, related to nothing, and being without the observer has no
quantitative parameters and measurements. It just exists! To determine those
parameters and measurements the observer is required. But he cannot say
anything about an oscillating source unless there are other oscillating sources
around. What the observer can do is to calculate the number of oscillations. If
he has other oscillators around he has a chance to compare. As a result of such
comparisons, he may find that some sources oscillate faster than others, i.e.
have higher frequency.
To systematize
the observation results they choose the most stable of the sources, and, for example
1000 ‘pieces’ of its complete oscillations are acknowledged as the initial
standard of duration, which is called the unit of period (time).
The standard of
period proves a useful instrument in systematization, allowing to assess any
sources of oscillations from a single intuitively comprehensible position.
Measurement: the ‘pieces’ (translator’s note: the author’s choice of term) of
oscillations in a single period. Thus, the observer has developed the first
measurement: ‘n’ pieces per 1000 pieces where ‘1000 pieces’ is the standard of
period (time). Such measurement can be given any name you like, Hertz, for
instance (pieces per second).


Fig.32. Unless extreme precision is required, a quartz
generator of signals could be used to set a standard of time.
Understandably,
any standard, including the standard of time, is no more than agreement based
on the very same oscillations: the unit of time is determined by an ordinary
number of oscillations of something. The initial measurement of a unit of time
are pieces! But for the sake of convenience a certain number of pieces of
oscillations of a certain, selected by consent, periodic process is called ‘one
second’ – 1 sec.
Rhythmus: Cool! Hertz are pieces divided by pieces. Velocity
are meters divided by pieces; acceleration – meters by pieces squared. If so,
we can equally measure both meters and kilograms in pieces… I wonder what
fault you find with the existing systems of measurements?
Dynamicus: But that’s how it actually is: everything is in
pieces! For example, the standard of time of 1 second is nothing more than the
length of 9192631770 pieces of oscillations of emission of quantum transfer
between the lines of the super-thin structure of 133Cs atom. As for
the standard of length, it, too, is measured in pieces of oscillations and
waves. A good proper measurement. ..
Establishment of
length standard, the modern definition of which requires the notion of ‘wave’
proved a more complex issue. Metrology sets as the standard of 1 meter 1650763.73
pieces of wave lengths of 86Kr which, again, fill in a certain
approved distance in space.
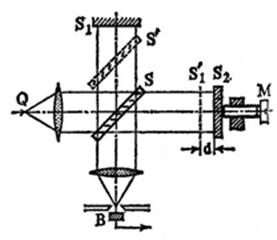
Fig.33. The draft of Michelson’s interferometer with a
regulated mirror used to count the waves. M – micrometric screw; B –
light-emitting diode used to measure light intensity.
The length of
traveling waves depends on the frequency of oscillations and the ability of the
wave medium to propagate waves with a certain speed in relation to itself.
According to the Doppler effect, in a system moving in relation to a wave medium,
the length of a traveling wave depends on the velocity of system, i.e.
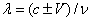 ; therefore it’s impossible to agree with a statement that a
distance accepted as 1 meter contains a constant number of the running waves of
86Êr emissions (transfer between the levels
of 5d5 –> 2p10).
; therefore it’s impossible to agree with a statement that a
distance accepted as 1 meter contains a constant number of the running waves of
86Êr emissions (transfer between the levels
of 5d5 –> 2p10).
The assertion
that the length of wave in the system doesn’t depend on the system’s speed is
correct only within the framework of Newton’s and Einstein’s theories which
deny the existence of wave medium as superfluous.
The issue of
establishing the length of electromagnetic wave in vacuum is awkward one. We
still do not know the direct way of measurement of the length of such wave in
progress. Nor do we know if it is possible even in theory to measure the traveling
wave directly.
Rhythmus:
That’s cool! How about the calculations and the work
of complex radio-electronic equipment? Do you really mean what you say? Using
the waves, they learnt to measure the distances to various planets and operate
space craft. To say nothing of the GPS navigation.
Dynamicus:
The impressive achievements you are citing cannot
confuse me. You’d better answer my question: when the system’s velocity changes
do the sound standing waves compress, or not? And if they do, why shouldn’t the
electromagnetic waves compress? If you are to say there’s no wave medium
(ether), prove it.
The standing
wave formed by the running direct and counter waves is quite the other matter.
It was proved earlier that the doubled length of the standing wave matches the
lengths of the traveling waves which form it only in one case: when the system
in wave medium is motionless ( ,
,
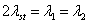 ). If the system is moving in the medium (
). If the system is moving in the medium ( ),
another relation would be correct:
),
another relation would be correct:
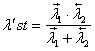 , (2.04)
, (2.04)
which doesn’t
indicate equality between the running waves and the doubled standing wave.
Therefore, when one speaks of the standard of length one should speak of the
number of standing waves in the space accepted as the standard of 1 meter. This
number is 3301527.46 of standing waves of 86Êr emission.
But a problem
emerges: when the system’s speed changes the behavior of the wave standard of
length present in it would be ambiguous because:
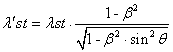 .
(2.05)
.
(2.05)
In other words,
if you take the rigid platinum-iridium standard and count the number of standing
waves fitting in the length of this standard when the system’s velocity in the
wave medium is zero ( ), then count them
again after the system’s velocity increased (
), then count them
again after the system’s velocity increased ( ),
the number of standing waves fitting the standard’s length would increase too.
Which is not observed in practice. In more than a century-long period of
improvement of the means of realization of the standard of length no increase
or decrease in the number of standing waves fitting 1 meter has been detected.
Why?
),
the number of standing waves fitting the standard’s length would increase too.
Which is not observed in practice. In more than a century-long period of
improvement of the means of realization of the standard of length no increase
or decrease in the number of standing waves fitting 1 meter has been detected.
Why?
Fig.34. Exterior view of the meter’s prototype (its
full length is 102 centimeters).
The reason why
it’s impossible to detect it can be explained by the dependence of the size of
the moving bodies on their speed in wave medium, following the rule:
|
Body size |
Standing wave length
|
|
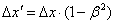
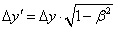
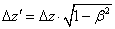
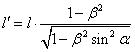 |
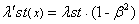
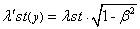
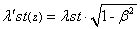
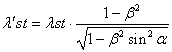 |
The hypothesis
becomes clear if the presumed compression of the body’s dimensions in the
moving system is compared with the compression of the standing waves in the
same system.
Fig.35. If the standard of length were matched with traveling and
standing waves, the situation with the establishment of the length standard by
counting traveling waves would become absurd. Another matter if standing waves
were counted. But with changed orientation in space or changed velocity regime
the standing waves compress. Had it not been for the material of the standard which
compressed in exactly the same way the standing waves compress, the number of
standing waves would change with the change of motion conditions. But this does
not happen.
Such
synchronization is possible only if the interatomic ties in a crystal lattice
have a wave nature, and can be presented in the form of standing waves.
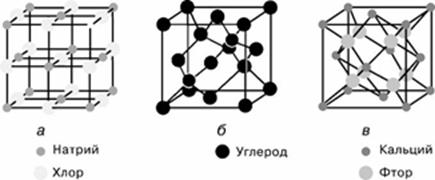
Fig.36. Crystals’ structure: a – halite NaCl; b
– diamond; c- fluorite CaF2. Made up of different atoms,
differently positioned, they all form a cube, i.e. relate to the same space
group.
If the inner
structure of matter were viewed in such a way, the distance between the atoms
would be always measured by the length of the standing wave. When the speed of
material bodies in a wave medium increases the standing waves shrink
(compress), which leads to a reduction of distance between atoms and
consequently to the reduction of the moving bodies’ dimensions.
Fig.37 Ties in a crystal (right) shown
as a package of standing waves in the nodes of which atoms are set.
Rhythmus: And what’s wrong with the Fitzgerald-Lorentz
contraction? What are the new contractions for if we have well-tested old ones?
Are you going to turn the tables on all?
Dynamicus:
The proposed model is based on a concrete phenomenon
called ‘compression of standing waves’. Whereas the Lorentz-FitzGerald
compression is based on a pure hypothesis which in modern physics became a
simple mathematical proportionality coefficient of Einstein-Lorentz.
Don't we need to
explain why the interatomic ties in matter should be presented as standing
waves? And why should atoms be positioned precisely in the nodes of the package
of standing waves and follow the nodes if these nodes, for some reason, change
their position in space?
This could be
done step-by-step: 1) examine the behavior of the model from positions of wave
geometry; 2) justify with the help of familiar classic theories the feasibility
of presenting the ties in matter as waves, and the matter itself as a package
of standing waves; 3) conduct an experiment and compare the results.
Let’s examine
the first step in which conditions are set from the
start by wave geometry.
Suppose we had
two coherent oscillators seeking, by condition, to occupy such a place against
each other in wave space so that along the imaginary line which connects them
the net emission would be totally absent. Such minimally possible relative position
is equal to the length of a standing wave (fig.38). Suppose the conditions of
stability were: oscillators set in the nodes of the standing wave created by
them; along the line linking the oscillators the outward emission is absent;
the number of standing waves (anti-nodes) between the oscillators is equal to
any uneven integer. Additional variable is the phase displacement between the
oscillators.

Fig.38. Along the line drawn between the oscillators
the outward emission is absent (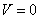 ,
,
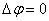 ).
).
If such system,
with its parameters unchanged, were moved in a wave medium with constant speed,
the interference pattern would change, i.e. the conditions of inner balance
would be broken (fig.39). We must find out by the change of which parameters we
can restore the balance conditions of the moving system of oscillators.

Fig.39 Inner balance has been broken. Outward emission
has emerged (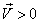 ,
,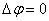 ).
).
To fully restore
the inner balance in the moving system one has to, first, change the distance
between the oscillators in accordance with 2.06; second, create the necessary
phase displacement between the oscillators (2.07)
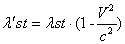 (2.06)
(2.06)
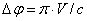 (2.07)
(2.07)

Fig.40 Thanks to the changes made (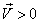 ,
,
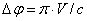 ) the inner balance of the system has been
restored.
) the inner balance of the system has been
restored.
but
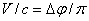 (2.08)
(2.08)
In which case
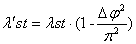 (2.09)
(2.09)
Which implies
that in a freely moving system its parameters: velocity, length and phase displacement
are closely related to each other, and must be mutually coordinated so as to
restore the balance.
So, we’ve found
that the motion of a system of oscillators in a wave medium leads not simply to
the reduction of distance between the oscillators, but also requires correction
of the phase displacement between the wave sources. The system’s velocity and
oscillators’ phase displacement have a positive correlation. If the motion
proceeds along the imaginary line linking the oscillators, then the distance
between the oscillators changes according to the rule:
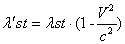 (2.10)
(2.10)
If the system of
oscillators is oriented across the movement, then, with phase displacement
absent due to its uselessness, the distance between the oscillators reduces
according to the rule:
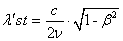 .
(2.11)
.
(2.11)
Conclusion:
modeling the material body as a package of waves in the nodes of
which the wave sources (atoms in material body) are set, we’ve pointed out the
geometric cause which leads to the longitudinal and traversal reduction of
measurements of the moving body, i.e. determined the algorithm of dimensions’
changes depending on the speed in the wave medium. Another important relation
has emerged: between the system’s velocity (in cases of only two oscillators)
and phase displacement of the wave sources in this system.
Let’s examine
another step, which is more related to real
dynamics. We are to examine the cause of oscillators’ preference to stay in the
nodes of a standing wave in cases when some external influence is attempting to
forcibly drive them out of the areas of stable balance.
According to
classical electrodynamics, atoms and molecules are interacting mostly via electromagnetic
forces. In solid objects the distance between atoms varies from 1 to 9
angstrom. Suppose, the ties were of electromagnetic-wave nature, and the
minimally possible distance between atoms is determined by a standing wave.
Let’s calculate the frequency at which this interaction is taking place.
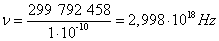 ,
,
which is by a
factor of ten to the power of four higher than the wave frequency of light band
(blue light frequency 6.3·1014 Hz) and corresponds to roentgen
frequency band. Which could imply that solid objects are, in essence, localized
clusters and sources of roentgen emission. In such case the question arises:
Why are these emissions practically unobservable?
Their
unobservability can be explained in the following way: all known ways of
measuring are based on the principle of comparison of received information with
a certain initial background standard which is accepted as mark ‘zero’; so if
black background were accepted as mark ‘zero’, any deviation from black is
observable; if the objects under study and the environment around them have the
same temperature, it would be impossible in such conditions to measure the
temperature of one object with the help of the other. The designed gadgets and
sense organs, being themselves the clusters of roentgen radiation, are
incapable of registering either the background state of space, or bodies of
similar frequency the amplitude of emission of which is equal to the background
amplitude but accepted as zero. In reality background level can be quite high,
but for us and our devices this level remains just the same the initial zero
reference point. That’s why we can observe only those objects whose emissions
in amplitude and frequency are higher than background one. It’s amplitude
excessive radiation which is registered by devices.
So, to detect
the standing waves which are in the background, i.e. assumed as zero, corridor,
band, of amplitudes and frequencies is practically impossible. Intuitively, we
understand that atoms, indeed, can form a primary structure made up of the very
same standing waves but their frequencies and amplitudes are a ‘blind spot’ for
devices. Everything which is going on in the background corridor can take
place, but cannot be directly detected. But there is a situation in which two
similar in chemical composition and structure objects can mutually register an
increase or decrease in each other’s emission in roentgen frequency band. This
is possible in gravitation field whose potential leads to a synchronized up or
down shift in all frequency parameters of the body. But in the planet Earth
conditions these shifts are extremely small, i.e. they are comparable with the
gravitational red shift for sources of any emission.
Rhythmus:
Does this mean we are the sources of roentgen
radiation? And everything around us are the sources of roentgen waves as well?
If so, why are we still alive?
Dynamicus:
Yes, we and everything around us are the sources
of roentgen waves. And our health almost immediately reacts to even insignificant
above the norm increases in precisely roentgen and higher frequency radiations
because all matter is made up of radiations of various frequency, saturated
with these frequencies, and for this reason their balance can be broken only by
the same or quite close in frequency excessive waves. If in isolated parts of
balanced wave system resonance emerges the system begins to change either
through self-adjustment or through self-destruction. For a human being such
resonance leads either to serious illness or death.
The matter is floating in a pool of
zero-gradient (background) radiation, and therefore there’s no means to measure
the level of such radiation.
The modern views
about the nature of interatomic ties are quite vague and exist at the level of
notions rather than models. The atom itself is no more than a convenient
pivotal notion with an array of experimentally determined properties. With discovery
of new properties the atom’s model changes (fig.41). There’s no definite answer
to the questions how exactly the atoms bind each other in a crystal lattice,
with what, by means of what processes?
Fig.41 Thomson regarded atom as electro-neutral system
of spherical form with a radius of about
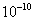 ì. The atom’s positive charge is evenly
distributed throughout the sphere’s volume, while negatively charged electrons
are set inside it. Rutherford & Nagaoka model of the atom.
ì. The atom’s positive charge is evenly
distributed throughout the sphere’s volume, while negatively charged electrons
are set inside it. Rutherford & Nagaoka model of the atom.
Suppose we had
two pulsating coherent oscillators which excite the wave medium creating a
standing wave between themselves. The oscillators are set in the nodes of this
wave, which results in a simple, minimally possible, stable system. Attempts to
bring the oscillators beyond the nodes areas trigger the reaction of a wave
field aimed at restoring the oscillators in their initial positions. If action
is aimed at only one oscillator, the whole system regroups and begins to move.
The whole chapter of this book will be devoted to this issue.

Fig.42 Dipole, triangle and tetrahedron are the most
stable systems because in-between the sources which form them only the integer
ties in the form of standing waves exist.
There can be
only three types of ideally stable wave systems with minimal dimensions: two
oscillators and a standing wave between them; three oscillators forming an
equilateral triangle with its side’s length equal to the length of a standing
wave; four oscillators in the form of tetrahedron with its edge’s length equal
the length of a standing wave (fig.43).
Fig.43
All other
geometric figures linked by standing waves have intersecting fractional ties in
the form of the very same standing waves. Fractional standing waves diminish
the system’s stability (fig.44).
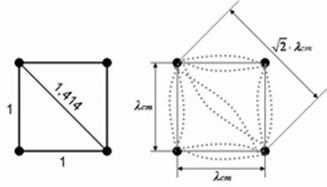
Fig.44



Fig.45 Energy distribution pattern: a) dipole b)
triangle c) square. Fig.45c shows that oscillators are in the
areas of unstable balance.
Let’s go back to
the issue of length standard. If during the motion compression of electromagnetic
standing waves takes place, then, comparing a certain number of these waves
with the standard of length we won’t find any compression. The standing waves
and the standard behave themselves in relation to each other as if nothing
happened with them, and no compression existed. Such situation makes one think
that interatomic ties of the standard and other bodies have electromagnetic
waves nature similar to a standing wave. Which explains the inability to detect
because both standing waves and the standard of length are subjected to equal
compression.
One should bear
in mind that both compression of electromagnetic standing waves as well as
contraction of dimensions of material bodies are only hypotheses based on the
established phenomenon of compression of standing waves in acoustics. The use
of this acoustics phenomenon as a direct analogy to electromagnetics is possible
due to similarity of the nature of oscillatory processes, nevertheless, we are
doing this only within the framework of developed models. The more so that
Rhythmodynamics itself is based on oscillations, wave medium and waves.
Back to contents ↑
§ 2.04 Dimension’s contraction and Michelson’s
experiment
Michelson’s
experiment is a good illustration to the contraction of dimensions and the
impact of this phenomenon on cancellation of expected results. Let’s examine it
in detail.
As we presume,
the interferometer’s size depends on its velocity in wave medium, according to
the rule:
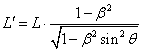 (2.12)
(2.12)
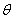 is the
angle of orientation of interferometer’s arm to the direction of motion
is the
angle of orientation of interferometer’s arm to the direction of motion
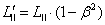 (2.13)
(2.13)
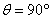
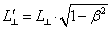 (2.14)
(2.14)
In these
directions the standing waves change their dimensions in the same proportion:
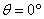
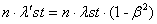 (2.15)
(2.15)
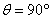
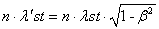 (2.16)
(2.16)
where ‘n’ is the
number of standing waves fitting in interferometer’s arms.
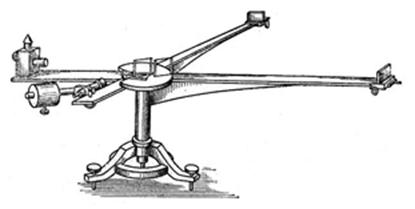
Fig.46 General view of Michelson’s first
interferometer.
If now we were
to repeat Michelson’s calculations, taking into account contraction of dimensions,
no difference in the beams’ time in transit would be found.
Dimension
contraction is absent, i.e. doesn’t depend on the system’s velocity V in
ether:
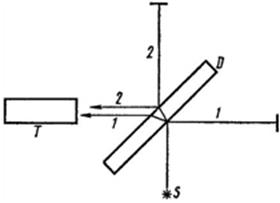
Fig.47. Interferometer’s general scheme
Let’s analyze
this experiment.
Suppose the
interferometer were positioned in such a way that beam 1 were moving
along the Earth’s movement, while beam 2 perpendicular to it. In such
case, unless ether is dragged by the Earth’s movement, the time the beam 1
travels its path is:
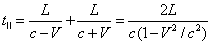 , (2.17)
, (2.17)
while the time
beam 2 travels its path is:
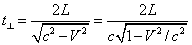 . (2.18)
. (2.18)
So, beams
1
and 2 spend different time to travel distance 2L and the time
difference is:
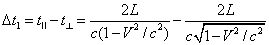 (2.19)
(2.19)
If we were to
turn the device by 90°, then, vice versa, the time
spent by beam 1 is:
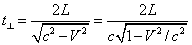 , (2.20)
, (2.20)
while the time
spent by beam 2 is:
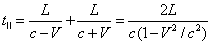 , (2.21)
, (2.21)
their
difference:
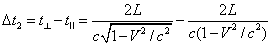 (2.22)
(2.22)
As a result the
interference fringes should shift, and though this shift amounts to
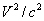 , it nonetheless is detectable. Consequently, having measured
fringes shift one can determine velocity of the ether wind on the Earth.
, it nonetheless is detectable. Consequently, having measured
fringes shift one can determine velocity of the ether wind on the Earth.
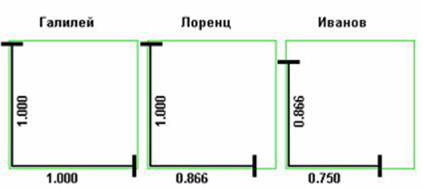
Fig.48 The length of interferometer’s arms depends on
the choice of type of dimensions’ contraction. Calculations are given for V=0,5c.
In
Rhythmodynamics the dimensions contraction follows the rule:
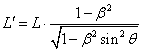 (2.23)
(2.23)
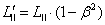 (2.24)
(2.24)
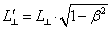 . (2.25)
. (2.25)
Then the time of
beam 1 in transit is:
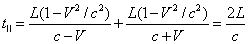 , (2.26)
, (2.26)
whereas the time
of beam 2
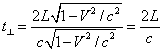 . (2.27)
. (2.27)
So, the time in
transit of beams 1 and 2 is equal, therefore
 (2.28)
(2.28)
In other words,
the time in transit (back and forth) of beams 1 and 2 depends
neither on the interferometer’s orientation to movement, nor its speed in the
wave medium, i.e. it’s always constant. It’s easy to show on the scheme used by
supporters of a different approach in explaining the cause of a slowing down time.
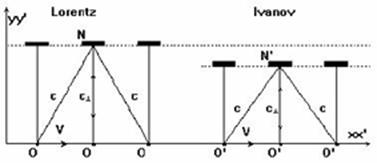
Fig.49 The scheme for calculating time slow down.
Lorentz’
contraction of dimensions implies that the traversal size doesn’t depend on
velocity V (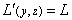 ), therefore calculating
the pace of time leads to a slow down of the clock pace in accordance with the
rule
), therefore calculating
the pace of time leads to a slow down of the clock pace in accordance with the
rule 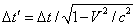 , i.e. a second in
the moving system lasts longer. In rhythmodynamics the traversal size changes
according to the rule
, i.e. a second in
the moving system lasts longer. In rhythmodynamics the traversal size changes
according to the rule
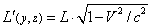 which removes the
problem of dependence of the pace of clock on its velocity, i.e.
which removes the
problem of dependence of the pace of clock on its velocity, i.e.
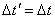 .
.
If the pace work
of identical clocks doesn’t depend on their velocities in the wave medium such
characteristic might be used to synchronize the clocks in different parts of
space so as to, for example, conduct experiment to determine the speed of
light in one direction. But first let’s give a rhythmodynamics’ interpretation
of the results of Michelson’s experiment.
Back to contents ↑
§ 2.05
Rhythmodynamics interpretation of the results of Michelson’s experiment
In this paragraph
we give a rhythmodynamics’ interpretation of the results of Michelson’s experiment
due to the absence of a strict or at least logically backed up solution of the
issue of electromagnetic ether as well as the Earth’s movement relative to this
so far incomprehensible wave medium.
Maxwell was the
first to raise the issue of a possibility of conducting an experiment which
could give a definite answer as to which of the existing theories was correct:
either an empty space of Galileo-Newton, or a space filled with luminiferous
ether. In this experiment the speed of light coming from a terrestrial source
on the moving Earth along its movement was first measured and then compared
with the speed of light measured when it moved in opposite direction. Apparently, unless the Earth drags with its movement
the ether around it, such speed in the first case is
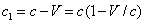 , in the second
, in the second
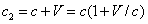 , where V is
the speed of the Earth. So, the difference of light velocity in the first and
second cases is of the first order of smallness
relative to
, where V is
the speed of the Earth. So, the difference of light velocity in the first and
second cases is of the first order of smallness
relative to  . Still, to conduct
such experiment one has to be able to measure the time it takes light to travel
a certain distance in certain direction, for example, in the direction of the
Earth’s movement. The task which is experimentally unsolvable due to the
problems of synchronizing clocks in various parts of space. Therefore in all experiments
staged on the Earth to determine the velocity of light this velocity was
determined by the time it takes light to travel forward and backward. Consequently, to determine the impact of the Earth’s
movement on velocity of light one has only to compare the time the light
travels, back and forth, a certain distance L one time along the Earth’s
movement, the other, say, in direction perpendicular to it. But in this case
the time difference in both the first and second cases would be of the second
order of smallness relative to
. Still, to conduct
such experiment one has to be able to measure the time it takes light to travel
a certain distance in certain direction, for example, in the direction of the
Earth’s movement. The task which is experimentally unsolvable due to the
problems of synchronizing clocks in various parts of space. Therefore in all experiments
staged on the Earth to determine the velocity of light this velocity was
determined by the time it takes light to travel forward and backward. Consequently, to determine the impact of the Earth’s
movement on velocity of light one has only to compare the time the light
travels, back and forth, a certain distance L one time along the Earth’s
movement, the other, say, in direction perpendicular to it. But in this case
the time difference in both the first and second cases would be of the second
order of smallness relative to
 , i.e. the magnitude
of order
, i.e. the magnitude
of order 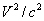 .
.

Fig.50 J.C. Maxwell
So, although
experiment could help solve the issue of ether’s behavior during Earth’s movement,
nonetheless smallness of the magnitude
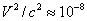 makes the
expected result extremely insignificant. In this connection Maxwell was rather
skeptical about actual possibility of solving the issue with the help of such
experiment. Nonetheless such experiment was soon, in 1881, staged by American
physicist Albert Michelson. To compare the time in transit of light traveling
both forward and backward along the Earth’s movement and perpendicular to it,
Michelson used interference phenomenon. For this very purpose he invented
interferometer which consisted of two mirrors N and M and a
semi-silvered mirror O positioned as indicated in the picture. A beam of
light from source S is split by plate O in two beams 1and
2
which after their reflection by mirrors M and N as well as
reflection of beam 2 from plate O get into microscope K. The
position of interference bars observed in the microscope is determined by the
transit difference which beams 1and 2 acquire during time period
when they travel the corresponding routes from plate O to mirrors N
and
M and backwards, which could be considered similar and equal to 2L.
makes the
expected result extremely insignificant. In this connection Maxwell was rather
skeptical about actual possibility of solving the issue with the help of such
experiment. Nonetheless such experiment was soon, in 1881, staged by American
physicist Albert Michelson. To compare the time in transit of light traveling
both forward and backward along the Earth’s movement and perpendicular to it,
Michelson used interference phenomenon. For this very purpose he invented
interferometer which consisted of two mirrors N and M and a
semi-silvered mirror O positioned as indicated in the picture. A beam of
light from source S is split by plate O in two beams 1and
2
which after their reflection by mirrors M and N as well as
reflection of beam 2 from plate O get into microscope K. The
position of interference bars observed in the microscope is determined by the
transit difference which beams 1and 2 acquire during time period
when they travel the corresponding routes from plate O to mirrors N
and
M and backwards, which could be considered similar and equal to 2L.

Fig.51 A. Michelson
The objective of
Michelson’s experiment was to turn the device by 90° and find the fringes’
shift indicating phase displacement and, thereby, the existence of motion in
ether. In 1981, when a theoretical analysis of Michelson’s experiment was
given, it was found that if the formation of the standing waves in OM and
ON arms of Michelson’s interferometer (fig.52) were examined, their length
 must depend on the angle
must depend on the angle
 of the
device’s orientation relative to the direction of movement and on the velocity
(V) relative to the wave medium (ether) in accordance with the formula:
of the
device’s orientation relative to the direction of movement and on the velocity
(V) relative to the wave medium (ether) in accordance with the formula:
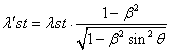 (2.29)
(2.29)
where:
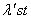 -
distance between the closest nodes of a standing wave in case of
interferometer’s movement;
-
distance between the closest nodes of a standing wave in case of
interferometer’s movement;
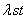 - distance
between the closest nodes of a standing wave in case of interferometer’s immobility;
- distance
between the closest nodes of a standing wave in case of interferometer’s immobility;
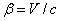 ,
,
where:
V – interferometer’s velocity;
c –
speed of light;
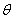 - angle of orientation between the
arm in which the standing wave is measured and the direction of
interferometer’s movement.
- angle of orientation between the
arm in which the standing wave is measured and the direction of
interferometer’s movement.
Fig.52. Michelson’s interferometer. N, M
– mirrors, O – semi-silvered mirror,
ÈÑ- light source,
ÈÊ – device to
observe interference pattern,
c1
– speed of direct
wave, c2 – speed of counter wave, c┴ – speed of wave perpendicular to motion, V
– interferometer’s velocity relative to ether, LII
è
L┴ – interferometer’s dimensions with V>0,
L0 – interferometer’s dimensions with
V=0.
In other words,
if Michelson’s interferometer changes speed or orientation relative to the direction
of movement in ether, the quantitative relation of standing waves must change.
The correctness
of this statement was proved in the experiment with sound standing waves: in
1990 a sound interferometer was built which registered, with the emergence of
wind, both compression of standing waves, according to (2.29) and changes in
their quantitative relation when the wind direction changed.
In Michelson’s
interferometer experiment no such direct measurements were conducted, but when
Michelson’s proposal about the length standard was implemented by
interferometer means [7], it was exactly the count of a number of standing
waves between the semi-transparent and reflecting mirrors which was mentioned.
No changes in the number of waves were ever detected, which made possible any
of the three options:
1.
Ether is dragged by bodies and it is completely
immobile on the Earth’s surface.
2.
Ether is always immobile; bodies move through
ether. Their dimensions change in such a way that the effect of motion through
ether is always unobservable.
3.
Ether doesn’t exist (assertion of the special
theory of relativity).
The correctness
of these assertions has been debated for over 120 years. Neither of the participating
sides has so far presented a convincing argument to back its position, though
each thinks it is right.
It’s worth note
that ether was originally assumed to be an immobile wave medium. Bodies were
thought to go through ether, being its disturbed state, i.e. ether freely
passes through bodies moving in it. Ether was characterized as a luminiferous medium
the speed of movement relative to which Michelson planned to determine with the
help of his interferometer. The absence of the positive result of his
experiment brought a justifiable question about the causes of inability to
experimentally detect motion in ether.
The hypothesis
of contraction of material bodies’ dimensions along the direction of movement
made it possible to explain the absence of a positive result, but it proved
insufficient because to be feasible it required introduction of another
hypothesis about the slowing down of time. Lorentz tried to give a theoretical
justification to this hypothesis but failed to find a phenomenon which could
have demonstrated the nature of contraction.
Such phenomenon
was found in 1981 following a theoretical analysis of the behavior of standing
waves in the systems moving relative to a medium, and it was called “standing
waves compression phenomenon”. In the light of the modern view on the wave
nature of matter, the standing waves compression phenomenon was transferred to
the electrodynamics of the moving bodies.

Fig. 53 Yuri Ivanov (1981 photo).
As a model, any
solid body can be considered as a package of standing waves, with atoms in
their nodes. Atoms are the sources of waves, and standing waves are the result
of interference. Any displacement of a node is thought to provoke the
inevitable shift of the appropriate atom.
Fig. 54 Velocity of a package of standing waves V=0
Dimensions of a package of standing waves with
V=0,7ñ
If such package
of standing waves is to change its speed relative to ether, the distance between
the nodes is to change too according to (2.29). This
would lead to contraction of the physical dimensions of the whole package,
consequently the body itself along all coordinates:
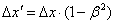
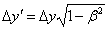 (2.30)
(2.30)
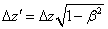
where:
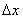 ,
,  ,
,
 – body dimensions with V=0
– body dimensions with V=0
Now, calculating the expected change in the number of standing waves
in the arms of Michelson’s interferometer, and taking into account contraction
of its size, we find that the result will always be zero. Similar calculations
of the difference of time of the beams in transit parallel and perpendicular to
the arms when interferometer is turned gave equally zero result.
Hence, the
contraction of interferometer’s dimensions is based on the physical phenomenon
of compression of standing waves (2.29) which was
transferred to material objects, assuming their wave nature.
The suggested
approach differs from a formal FitzGerald-Lorentz hypothesis of length contraction
by the fact that it’s based on the physical phenomenon: compression of standing
waves.
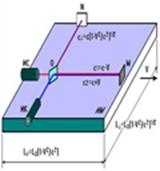
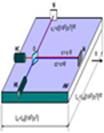
Fig.55 Interferometer’s size change by Lorentz (left)
and in accordance with compression of standing waves (right).
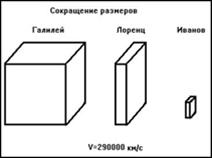
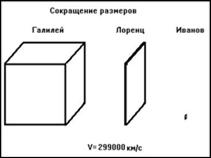
Fig.56 While the objects approaching the speed of
light turn, according to Lorentz, into ‘flying pancakes’, according to Ivanov
they turn into dots.
Lorentz
hypothesis of length contraction was suggested exclusively for the sake of
rescuing the idea of ether.
Ivanov’s
contraction of dimensions along all coordinates is based on the physical phenomenon:
compression of standing waves. Velocity increase triggers
compression of an object.
The physical
nature of the new explanation allows to talk about the special theory of
relativity as an intermediary hypothesis advanced because of initial inability
to explain the results of Michelson’s experiment within the framework of
classic concepts. Now we have grounds to reject the Einstein’s principle of
invariance of the speed of light and replace it with the principle of illusion
of invariance of the speed of light (within the framework of new transformations
of dimensions and coordinates such illusion is inescapable). The geometry of
wave and inside-matter processes is such that the observer has no opportunity
to detect through direct experiment violation of invariance theory due to a
compensatory effect caused by compression of dimensions of moving objects.
Derivation of
a formula describing the behavior of parameters of a standing wave in
conditions of the system’s motion relative to a medium:
To substantiate
the claim of discovery one has to observe a number of mathematical procedures,
actually to solve the standing wave equation in the case when the emitter and
reflector are moving in ether with equal speed V.
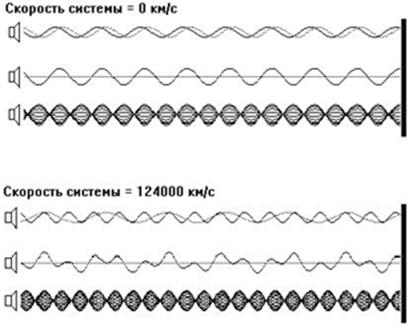
Fig.57 Emitters’ frequency is constant. With the
device’s velocity increase relative to medium, and in accordance with Doppler’s
rule, the direct and counter waves change their lengths (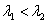 ). For the inside observer
in
the system which changed speed the frequencies of these waves will remain equal
(
). For the inside observer
in
the system which changed speed the frequencies of these waves will remain equal
(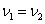 ) but the nature of interference is to change, which
is to lead to contraction of distance between the neighboring nodes, standing
wave length change, and increased number of standing waves. The package of
standing waves compresses.
) but the nature of interference is to change, which
is to lead to contraction of distance between the neighboring nodes, standing
wave length change, and increased number of standing waves. The package of
standing waves compresses.
For the sake of better
illustration the process of standing wave formation is split in three parts:
·
the upper draft shows direct and counter waves
and dependence of their length on speed;
·
the middle draft shows the result of waves’
superimposition (resultant);
·
the lower draft shows the sum of resultants
during the full period.
It was
established that with the change of speed of the system ‘source-mirror’ the
form of the resultant and the distance between nodes change too, which leads to
compression of the package of standing waves according to the rule (2.29).
Derivation of
a standing wave equation for the system moving in medium:
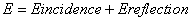
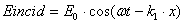
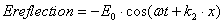
where:
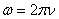
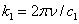
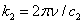
then:
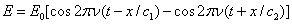
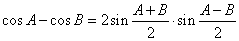
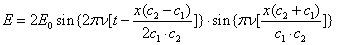
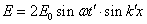
where
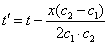 (2.31)
(2.31)
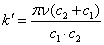
but
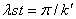
then
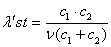 (2.311)
(2.311)
but
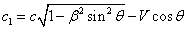
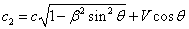 (see derivation
below)
(see derivation
below)
Putting
 and
and  values in formulas (2.31)
and (2.311) we obtain expression for
values in formulas (2.31)
and (2.311) we obtain expression for
 and
and
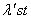 for any orientation of a standing wave in the moving system:
for any orientation of a standing wave in the moving system:
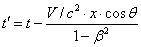 (2.32)
(2.32)
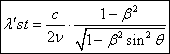 (2.321)
(2.321)
With  è
è
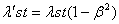
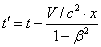 . (2.33)
. (2.33)
With
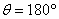 è
è
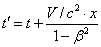 . (2.34)
. (2.34)
The time of the beam in transit forward and backward:
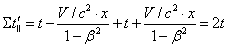 .
.
With 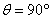 è
è
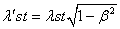
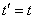 (2.35)
(2.35)
With
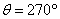 è
è
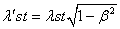
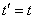 (2.36)
(2.36)
The time of the beam in transit forward and backward:
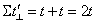 .
.
Result: 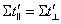 (2.37)
(2.37)
Which means
that:
1.
The moving object which constitutes a package of
standing waves changes its longitudinal dimensions
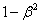 times,
traversal
times,
traversal  times, which
strictly matches compression of standing waves in these directions.
times, which
strictly matches compression of standing waves in these directions.
2.
The overall time of the beam in transit forward
and backward along the arms of Michelson’s interferometer does not depend on
the device’s velocity and orientation and is always equal to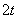 .
.
3.
The pace of time doesn’t depend on the system’s
velocity and is equal in all identical systems, no matter whether they are
moving relative to wave medium (ether), or stay put.
These formulas
point directly to the solution of the problem linked with the negative results
of Michelson’s experiment. Historically, it was the absence of a phenomenon
which could have been used as explanation that made science adopt relativity
theory which ends in a deadlock.
The scheme to
calculate velocity of a wave front relative to moving source
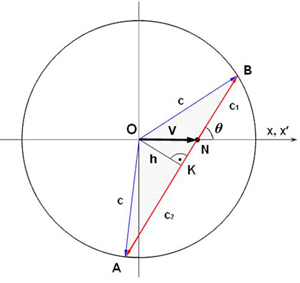
Fig. 58
In which:
N – moving source
V – source velocity
Î
– coordinate of the place where the wave front is emitted
ñ
– velocity of wave front
ñ1 – velocity of wave front
relative to N
ñ2 – velocity of wave front
relative to N
Calculations
of the wave front velocity relative to the moving source
AK=KB;
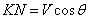 ;
;
 ;
;
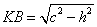 ;
;
c1=KB–KN;
c2=KB+KN.
Calculations results:
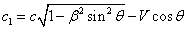 (2.38)
(2.38)
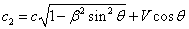 (2.39)
(2.39)
Let’s describe an acoustic experiment confirming validity of the
discovered rules. There is a problem of transfer from the results obtained in
acoustic experiments to electrodynamics. Had our predecessors (Michelson in
particular) known about the compression of standing waves in acoustics they
would have planned their experiments not to determine
velocity in ether but to
discover the compression of standing waves. In other words, the negative result
would have been interpreted not as ether’s absence, but as confirmation of
compression of interferometer’s dimensions. Now we know that experiment with
the aim of discovering motion in luminiferous medium should be planned
differently.
Experiment
with the sound standing waves
In the summer of
1990 a series of experiments were conducted with the sound standing waves. The
experiments proved beyond doubt that with the increase of wind speed relative
to immobile emitter of sound oscillations and reflector (mirror) a compression
of the package of standing waves takes place.
Fig.59 Calm weather (a) and strong wind (b). The
sources of sound were powered from a single generator.
With the
emergence of wind the lengths of sound waves and their velocities are changed according
to the Doppler’s principle. The wave frequency in the system of sources remains
constant.
For
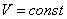 ,
, 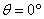
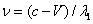 ;
;
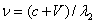 (2.40)
(2.40)
The waves of
different length but of equal frequency interfere, resulting in a standing wave
the length of which
 (2.41)
(2.41)
For
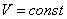 ,
, 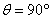
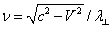 (2.42)
(2.42)
The waves of
equal length and equal frequency interfere, resulting in a standing wave the
length of which:
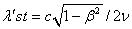 (2.43)
(2.43)
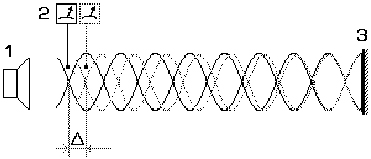
Fig.60 The key diagram of experiment with sound.
In calm weather
a standing wave emerged between emitter 1 and mirror 3 (as a
rule, experiments were conducted during a spell of quiet before a
thunderstorm). With the help of indicator 2 a node of the standing wave,
shown by unbroken line, was registered. With the emergence of wind the shift of
control node toward mirror 3 was registered. The observed effect was
interpreted as compression of the package of standing waves (the compressed
package is shown by dots).
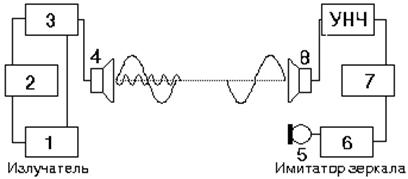
Fig.61. Block diagram of the device used in the
experiment: 1 – sound generator; 2 – frequency multiplier (x4) serves to form a
pilot-signal; 3 – mixer; 4,8 speakers; 5 – microphone to receive the
pilot-signal; 6 – divider ( ); 7 restorer of the basic signal.
); 7 restorer of the basic signal.
Mirror simulator
made it possible to create a pseudo-coherent emitter and thereby extend the
experiment’s base two-fold, which significantly increased sensitivity of the
device.
The frequency
magnitude of the driving generator was not important in the experiment. So it
was set for the wave length to amount to 10 cm., while the distance between the
speaker and mirror was 70 meters. With the emergence of wind a 5 cm. shift of
the control node toward the mirror was registered which corresponded to wind
velocity of 30 km/h. There were even greater shifts, but the main result of the
series of experiments was the clear-cut rule: with the emergence of wind the
package of standing waves compressed no matter whether the wind was blowing
along or across the device.
Conclusion
Discovery of
compression of standing waves and application of this phenomenon in electrodynamics
of the moving objects in non-entrained ether has again raised the question of
existence of ether as a wave medium.
Back to contents ↑
§ 2.06 The speed of light in one direction
Synchronization
of the clocks’ pace
The task of
synchronizing the running of the clocks A and B is limited to
their start with the help of clock C moving with constant speed from A
to B. The moment the running clock C
draws level with the
stopped clock A, the clock A is started in a way so that it
should show exactly the same time the clock C shows. The moment the
clock C reaches and draws level with clock B, the clock B is
started in a way so that it should show exactly the same time the clock C
shows. Thereby the synchronization is accomplished.


Fig.62 Synchronization with the help of the even
transfer of the clock. Synchronization procedure for the clocks positioned in
different parts of space is limited to the start of clock A and
communication of its time reading to clock B via clock C by way
of its even transfer.
Now, if synchronization has succeeded, one can begin determining the
system’s velocity in ether. To do this one has to register the signal’s time
in transit from A to B by B clock which will be
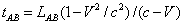 , after which from B to A by A clock which will
be appropriately
, after which from B to A by A clock which will
be appropriately
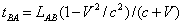 .
.
But
 (2.44)
(2.44)
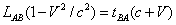 (2.45)
(2.45)
Equating the
right parts
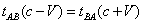 (2.46)
(2.46)
we’ll solve the
equation relative to V
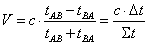 (2.47)
(2.47)
Having assumed
a random distance between the clocks A and B and measuring time
of the signals in transit in accordance with the experiment conditions we can
determine the system’s velocity in ether.
Thus one can
solve more than a century old dispute about possibility of measuring the speed
of light in one direction. Such experiment could either strengthen position of
the theory of relativity regarding the existence of luminiferous ether or
expose the theory’s faults. It’s only experiment which is needed.
Experiment
calculations
Solving this
specific task we are to show that during synchronization of the readings of the
clocks in different parts of space with the help of the third evenly going
clock it doesn’t actually matter whether the pace of time in the moving clocks
slows down or not.
Suppose the
distance between clock A and clock B were 100 km. Suppose
the pace of time of the moving clock C depends on its speed following
the rule 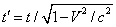 , where
, where
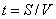 . Suppose the speed of clock C transfer from A to B
equals 100 km/h (0,02778 km/sec).
. Suppose the speed of clock C transfer from A to B
equals 100 km/h (0,02778 km/sec).
Then according
to the clock C which moved from A to B clocks less time
will pass: 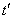 =3600 ·
0,99999999999999571262= 3600,000000000015434568sec.
Which means that clock B synchronized with the help of clock
C
will be behind clock A by
=3600 ·
0,99999999999999571262= 3600,000000000015434568sec.
Which means that clock B synchronized with the help of clock
C
will be behind clock A by
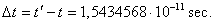
Suppose the
velocity of the Earth were 30 km/h. and its vector were the same as the
direction of imaginary lines between the clocks A and B.
Then the time in
transit of the light signal from A to B by B clock would be
 =0,00033336667sec., and from B to
A by A clock would be
=0,00033336667sec., and from B to
A by A clock would be
 =0,00033330000
sec. If the clocks and combined with them sources
of signals were orientated along the movement in ether, then with the Earth’s
re-orientation in space due to its rotation along its axis and its movement
around the Sun the
=0,00033330000
sec. If the clocks and combined with them sources
of signals were orientated along the movement in ether, then with the Earth’s
re-orientation in space due to its rotation along its axis and its movement
around the Sun the
 and
and
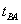 would change their values with the period of 12 hours.
would change their values with the period of 12 hours.
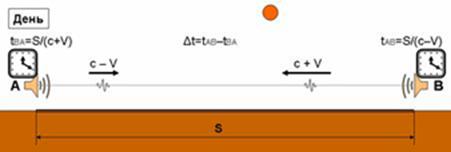

Fig.63.
The difference
between the time of light passing distance AB with speed c-V by
clock B and distance BA with speed c+V by clock A
emerges in the 8th digit after dot – which is possible to
register by modern instruments. It must be noted that clocks A and B
have
a presumed de-synchronization in the 11th digit after dot.
This de-synchronization is too small to have a significant impact on the
results of expected measurements.
Another option
could be experiment without special synchronization of the readings of clocks A
and B positions in different parts of space on condition that these
clocks have maximally equal pace and thereby ensure the stability of frequency
of the short impulses emitted by sources. The main task of the experiment is to
detect the point (the spot) where impulses meet, being emitted by the source A
to B and B to A. In the course of watching this point of
impulses’ meeting its daily shift caused by the Earth’s rotation in ether is
expected.
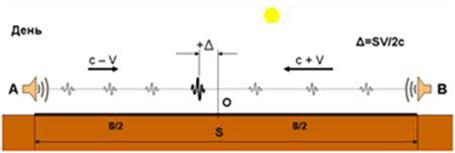
Fig.64
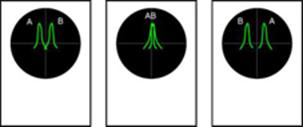
Fig.65
For example,
with the Earth’s velocity in ether of 30 km/sec., the distance between
the sources of 60 km and correspondence of the shortest possible
line between the sources and velocity vector, the expected daily fluctuation of
the point of the impulses meeting (crossing) would amount to
±3m. With the speed of solar system of 300
km/sec., velocity magnitude which some sources refer to, the expected daily
fluctuations are to reach ±30m.
Fig.66. Experiments’ results depend on the Earth’s
orientation to the motion in ether.
Conclusion.
With existing theoretical possibility of detecting the system’s own
motion in electromagnetic wave medium (‘absolute speed’) it would be quite
absurd to refuse the necessity of detecting such motion as well as deny the
existence of the wave medium.
Back to contents ↑
§
2.07 RD transformations
of coordinates
|
According to Galileo
|
According to Einstein-Lorentz |
According to Ivanov |
|
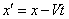 |
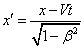 |
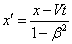 |
|
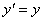 |
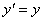 |
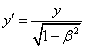 |
|
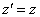 |
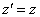 |
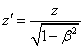 |
|
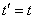
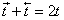 ? ? |
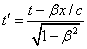
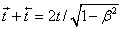 |
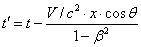
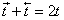 |
One should make
distinction between the contraction of dimensions and transformation of
coordinates: dimensions refer to a real object, coordinate transformations – to
mathematical manipulations to suit the principle of subjective invariance.
Back to contents ↑
§ 2.08 Lively standing wave
The
‘lively’
standing wave effect was discovered following the discovery of the standing
waves compression.
While equality
of frequencies is the main condition for the emergence of a standing wave, this
equality is always realized when the falling and reflected waves are present.
And it doesn’t matter whether the surface which reflects waves is moving or
not.
For example,
observer is placed between the two coherent sources. If his velocity is zero,
he registers a regular standing wave. If the observer is moving in his reference
frame the standing wave will be perceived as a
beat (fig.71). But what is to happen if the wave reflector moves along with the
observer?
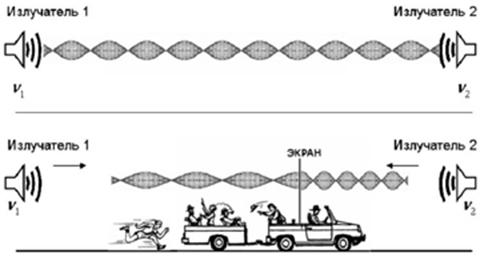
Fig.67. Coherent emitters ( ). The standing wave moves along with screen; its
parameters have changed. The standing wave with changed parameters exists only
for the moving observer, that’s why we call it the ‘lively standing wave’. If
the observer changes his speed, the parameters of the standing wave are to
change too.
). The standing wave moves along with screen; its
parameters have changed. The standing wave with changed parameters exists only
for the moving observer, that’s why we call it the ‘lively standing wave’. If
the observer changes his speed, the parameters of the standing wave are to
change too.
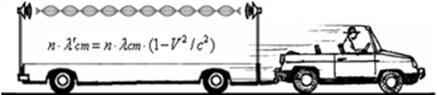
Fig.67.1 The standing wave also takes place when
coherent sources are moving in wave medium. With the increase of the system’s
velocity the distance between the nodes is to shrink and emergence of
additional anti-nodes will be observed, i.e. a package of standing waves is to
compress.
Phase
displacement
Let’s examine
the behavior of a standing wave emerging from wide-apart sources which are
motionless in medium. A package of standing waves has emerged between the
coherent sources. There’s no phase displacement between them too. In such
situation the interference pattern will be symmetrical. Let’s mark the position
of the central anti-node.
A phase
displacement between the oscillations is created. Apparently, the nodes and
anti-nodes’ position is to shift relative to their initial position. (fig.68).
With the growth of phase displacement nodes and anti-nodes of the standing wave
are moving farther from their initial position, and with the phase displacement
of 180° they’ll shift half of the standing wavelength. Further phase
displacement will lead to further standing wave shift.
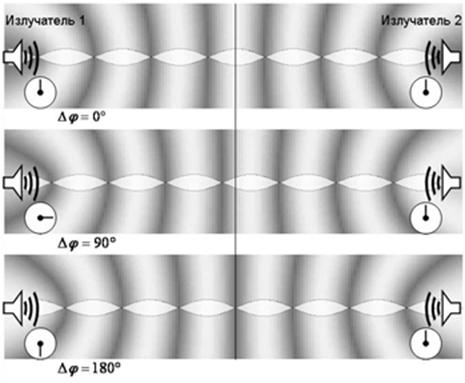
Fig.68 Phase displacement leads to the shift of nodes
and anti-nodes.
If, by
definition, the standing wave propagates no energy in space, then, changing the
phase displacement, we organize such propagation: phase displacement between
the sources leads to energy transfer in space between the two sources.
But constantly
changing in time phase displacement between the sources means frequency
difference
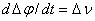 (2.48)
(2.48)
Which means that
existence of frequency difference between the sources leads to the standing
wave energy transfer from the source of higher frequency to the source of lower
one. Energy transfer (flow) is taking place.
Back to contents ↑
§ 2.09 Frequency difference and the speed of energy
flow
Watching the
conduct of a standing wave in a situation when phase displacement changes in
time, we found that increase in phase displacement leads to standing wave
shift, while the constant phase displacement in time is nothing but frequency
difference (2.48).
This relation
shows that the more frequency difference the higher is the speed of standing
wave shift. To determine this speed one has to find a moving system in which
the standing wave shift will be absent. Which is only possible in a situation
when in the moving system the waves coming from the sources have equal
frequencies (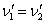 ).
).
Let’s explain it
the following way.
Suppose we had
two sources of waves with frequencies correspondingly
 and
and 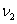 . Suppose
. Suppose
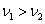 . One has to determine the speed of the system in which the
frequencies
. One has to determine the speed of the system in which the
frequencies
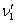 and
and
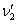 of waves coming from the sources are equal.
of waves coming from the sources are equal.
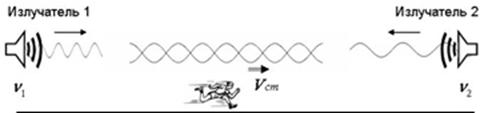
Fig.69 The observer has to move to implement the
condition of frequency equality of the waves coming to him. In this case he
registers the standing wave!
In the moving
system we have
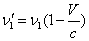 (2.49)
(2.49)
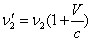 (2.50)
(2.50)
But
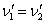 , therefore
, therefore
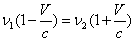 (2.51)
(2.51)
Let’s solve the
equation relative to the speed of the system in which a genuine standing wave
was observed:
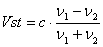 (2.52)
(2.52)
The same is the
speed of energy flow in the standing wave. But standing it is only for the observer
who moves with the same speed as the wave does.
Rhythmus:
Fig.69 shows different wavelengths. Which means
different frequencies too?
Dynamicus: Relative to the moving observer the frequencies of
direct and reflected waves are the same But we are dealing with the movement of
the system in medium, which implies the Doppler effect.
Hence these effects.
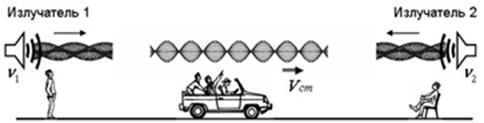
Fig.70 Frequency difference takes place (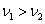 ). The speed of energy flow and the speed of the car
are equal. The passengers in the car observe a standing wave, and for them the
energy transfer doesn’t exist. The observers outside see a complex wave picture
which is not a standing wave.
). The speed of energy flow and the speed of the car
are equal. The passengers in the car observe a standing wave, and for them the
energy transfer doesn’t exist. The observers outside see a complex wave picture
which is not a standing wave.
Rhythmus:
So, what you say is that there is a standing wave for
those who are running or riding, and there is none for those who are standing
or sitting?
Dynamicus: Yes, that’s the meaning of this phenomenon, and
that’s what baffles everyone creating invariance illusion among moving observers,
especially if they deal with electromagnetic waves. The significance of the
illusion lies in the fact that nothing seems to change for the observer.
Whereas actually all the phenomena and processes change, but in such
coordinated way that it would be a real problem to detect those changes.
Rhythmus: But in electrodynamics we can measure the length of direct and
reflected waves, and thereby detect changes…
Dynamicus:
Unfortunately, I so far haven’t heard of experiments
in which direct measurements were made of the length of traveling electromagnetic
waves. We still estimate the length of the wave referring to the length of the
standing wave, which is not the same, as you now know. The standing wave may
emerge as a result of superimposition of waves of equal frequency but of
different, due to Doppler’s effect, length. So until now the general view of
the standing wave should now be regarded as a specific case for
V=0.
Now let’s go
back this part of the standing wave definition which refers to the absence of energy
propagation in the standing wave. And how electromagnetic standing wave is to
behave? Will the energy flow inside the electromagnetic standing wave be in
this case identical to the electric current in electricity cable? Let’s have a
simulated experiment.
Fig.71 Frequency difference is absent. The flow of
energy in the system of motionless observers is absent. In the system of moving
observers relative to standing wave the energy flow exists. The of energy flow
velocity equals in modulus the car velocity. Could it be the source of de
Broglie waves?
Suppose we had
two sources of electromagnetic waves (300mHz)
set wide apart in space. A standing wave emerges between the sources of equal
frequency. The observer putting a neon indicator in the node would register
absence of energy flow. Which means for us that the energy flow speed both
relative the observer and wave medium is zero.
The position of
neon indicator is fixed in the node. Let’s
increase the frequency of one of the sources by 0.1 Hz. The standing wave would
start moving slowly. Which will be visible from the increasing brightness of
the neon indicator. Theoretically, the speed of such transfer will be:
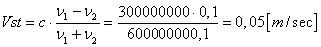 .
.
The velocity
magnitude is not big, so one can observe the node’s transfer by ‘catching’ manually
the node with the neon indicator and following it. The speed of indicator
following the node will be close to the calculated one, i.e. 5 cm/sec. If frequency
difference were increased ten times, which is to amount to 1 Hz, the speed of
node transfer, as well as the whole interference process, will also increase
ten times reaching 0.5 m/sec. For us it would mean that the speed of the energy
flow in the standing wave equals 0.5 m/sec.
Suppose, the
observer were moving in the same direction with the same speed (0.5 m/sec) with
which the standing wave is moving. Relative to the moving observer the nodes
and anti-nodes would be immobile, therefore he registers absence of energy
flow. He also registers that the waves coming to him have equal frequencies,
i.e. he doesn’t detect frequency difference.
Rhythmus:
One can catch up with electric current in electricity
cables, it seems, right? If the commuter train were moving with the speed of
current in the cables, the commuter’s electric engines would stop running,
right? And how about the alternating current? What is its speed?
Dynamicus: One shouldn’t mix up the electric current and the
current created artificially by electromagnetic energy. The given example shows
clearly how the energy flow is formed and why the speed of this flow can be
different. As for the alternating current, it is the same old direct current
moving in reciprocating fashion. To understand this one has to carefully
examine the work of electric generator. Than it will become clear that it’s not
the current but information signaling the start of the motion or the change of
direction of the current in the medium which propagates with the speed of
light.
Apparently,
significant increase in frequency difference would lead to significant increase
in the speed of the energy flow. For example, the two-fold frequency difference
(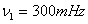 ,
, 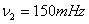 ) would produce the
energy flow velocity of
) would produce the
energy flow velocity of
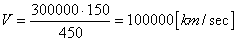 .
.
If anti-nodes of
the standing wave were rushing past us at such speed, the energy transferred by
them would look to us like a continuous flow. But now we know that this flow
has a definite speed and understand why this speed differs from the maximum
possible magnitude which equals the speed of light. We also know why the energy
flow always moves toward the source of lower frequency.
Here’s a real
life example. “On Feb.14, 1996 an energy disagreement took place in the
single energy system of Russia and Ukraine. Following a suspension in the work
of atomic power station in southern Ukraine a frequency lowering took place in
Ukrainian part of the energy system which triggered the influx of energy from Russia where frequency was higher. To preclude energy losses the Russian side was forced to
switch itself off Ukraine.”
Back to contents ↑
§ 2.10 On nature of electric current
Let’s consider
the content of this paragraph as a hypothesis based on the results of examining
the issue of the speed of electromagnetic energy flow.
Assuming that
direct electric current emerges due to natural frequency difference of
materials used, say Cu-Zn, one may be tempted to
determine the direction of movement in the circuit. But here the researcher may
run into difficulties. First, the energy flow may be formed at various
frequencies simultaneously which would lead to the energy flow with indefinite
speed (its speed will be higher at some frequencies, but lower at others).
Here’s a simulated
experiment. Suppose, we had two similar sheets of copper suspended on kapron
strings near each other at the same height from the Earth. Let’s measure the
difference of electric potentials between the sheets with the help of a
sensitive device, for the purpose of which one has to connect the device
preferably simultaneously to both sheets.
After which one
of the sheets is replaced by a zinc one, and measurements are repeated.
The following
results could be expected:
1.
In the first case when electric potential was
measured between two sheets of copper no current was registered.
2.
When electric potential between copper and zinc
sheets was measured the device registered a brief presence of current.
What’s the
cause? Why is there no current between the sheets of similar material, and emerging
current between the sheets of different, zinc and copper, materials?
To explain the
absence of current in one case and its emergence in the other let’s go back to
the previous paragraph where the cause of energy transfer is explained by the
frequency difference between the sources. Which means that copper sheets at
their atomic level have equal frequency parameters, while zinc-copper sheets
have different frequencies.
The same method
could be applied to test all elements of Mendeleyev periodic table.
***
We are paying
much attention to standing waves because within the framework of rhythmodynamics’
methods they are the main link and measure during self-organization of systems.
With their help we are to model the processes participating in formation of
these systems’ transfers, emergence of inertia properties and force
interactions between the elements of the system, and between the systems.
Conclusions
Rhythmodynamics
helps create the models of phenomena. One of those phenomena is compression of
standing waves which gave justification to renewed interpretation of the
results of Michelson’s experiment. It was convincingly shown that rejection of
the notion of wave medium (ether) proved unsubstantiated. A new model of Michelson’s
experiment interpretation was proposed based on the system of oscillators in
the wave medium.
Back to contents ↑
Chapter 3. Fundamentals of Self-organization
Self-organization
is a way of the world’s existence. But what lies at its basis, what processes
ensure self-organization, what’s its mechanism?
Any action
understandably requires energy. Comparing those energies they talk of some
measure, but so far no answer has been given to
the question: what is energy, where’s its source and what are the source’ intentions?
§ 3.01 Energy as measure of motion
Energy is the
universal measure of motion of matter, i.e. a certain magnitude showing how
much motion is present in this or that object at a given moment, irrespective
of the nature of motion. Any transfer in wave medium is regarded as motion.
Back to contents ↑
§ 3.02 Absolute and relative aspects of energies
The postulates
of modern physics and theories based on them do not allow for absolute notions:
energy, speed, time, frame of reference. The postulates of rhythmodynamics and
wave geometry, on the contrary, suggest impossibility of creating a clear
physical picture of the world without the carrier of constructs in geometry and
wave medium in rhythmodynamics. The advantage of rhythmodynamics’ approach is
in its ability to use both absolute and relative notions. For example, the
objects’ speed in wave medium is absolute, the speed between the objects is
relative. The same applies to energies: the higher is the object’s speed, the
greater is the absolute value of its kinetic energy; if another similar object
were moving alongside it, we, comparing kinetic energies, could only speak of
their difference. In that case kinetic energy is only relative. One should constantly
remember that any relative magnitude is the result of the difference of two
absolute magnitudes. For example, the relative speed of two planes 100 km/h. which means equation for a simple case
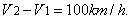 where V1
and V2
are velocities relative to air (for planes this velocity
is the absolute parameter). The frame of reference linked with air is absolute
for a plane, but if you are inside the plane and see no outside points of
reference you cannot say anything about the plane’s absolute speed. It can be
any.
where V1
and V2
are velocities relative to air (for planes this velocity
is the absolute parameter). The frame of reference linked with air is absolute
for a plane, but if you are inside the plane and see no outside points of
reference you cannot say anything about the plane’s absolute speed. It can be
any.
We think the
world around us exists in the form of electromagnetic waves. We cannot say with
any certainty that at this level of its organization its phenomena are realized
by continuum, so it would be more appropriate to speak of electromagnetic wave
medium as the closest foundation. It’s this foundation which should be called
absolute reference frame (ARF) because for material and other wave objects of
our world it performs the same role of the air for the plane. Then all movement
should be regarded as taking place in electromagnetic medium relative the
reference frame linked to this medium. The tricky question of determining one’s
own speed in wave medium emerges. The modern level of development of the
standards of measures allows to solve this task, which is actually limited to
determining the speed of light in one direction.
Rhythmodynamics
regards energy as ‘capacity’. This capacity can be potential, hidden till the
necessary moment, or kinetic. Kinetic energy is always linked with motion and
in rhythmodynamics is divided into ‘absolute’ and relative. This is connected
with wave medium which plays the role of the foundation for the objects present
in it. The system of coordinates playing the role of absolute reference frame
is linked to the medium.
To reveal the
mechanism’s essence of kinetic energy, i.e. to transform of the notion of
energy into model ideas at the level of processes, one has to solve two basic
problems:
1)
to establish processes which trigger the
self-organization of similar elements into objects;
2)
to establish parameters and their changes which
self-organize the motion of objects.
Back to contents ↑
§ 3.03 Self-organization of wave systems
All objects in
nature, just like the nature itself, are self-organizing systems. There are
many examples of self-organization both in macro and micro worlds: self-formation
of galaxies and planetary systems of the Sun type, crystals’ growth, chemical reactions,
the growth of living organisms, social processes. But how exactly does
self-organization proceed, what processes lie at its foundation, are there
general algorithms?
For example,
atoms in bodies have no direct contacts between
each other being quite apart from each other and form space lattice. There’s
only one possible explanation to such atomic ties: they are connected with each
other by electromagnetic wave fields. The sources of those fields are atoms
themselves and their nuclei.
But how does
this tie between atoms emerge, on the one hand, capable of keeping them at a
certain distance from each other, i.e. preventing their merger, on the other,
preventing them from darting apart?
Before we begin
examining this important issue, let’s clarify the meaning of the terms: wave
source and oscillator. Oscillator in our view is a geometric object, a dot; a
source of waves is an object of rhythmodynamics of the smallest possible dimensions.
While with the help of dot-sized oscillator the researcher may detect position
of potential’s hole in the carrier of constructs, i.e. while the oscillator, by
condition, follows in the wake of the hole, the wave source, which has
dimensions, acquires ability of assessing gradients which lead it to the
nearest potential’s hole. It’s worth note that wave geometry is the basis of
rhythmodynamics.
Here’s a typical
example for detailed inspection.
Suppose, there
were two sources of waves positioned within the range of each other’s emission
with in phase oscillations. The waves are coherent, have no frequency beat, and
form a standing wave between the sources. The sources have occupied stable
positions in dynamic holes of potentials (areas of comfort) at a distance of
one standing wave length. An elastic tie has emerged between the sources. Let’s
examine the processes which take part in this tie formation.
Three objects
are taking part in the process: two sources and wave medium (in wave geometry –
two oscillators and carrier of constructs). The waves emitted by the sources
after their departure become independent formations, i.e. have no link with the
sources and exist on their own. The waves intersect and form a field of
alternating amplitudes in the shape of nodes and anti-nodes, while along the
imaginary line between the sources a standing wave emerges.
We presume that
for a source the standing wave node becomes area of stable balance, a potential’s
hole, the area of comfort. The source can react only to the wave field around
it, and if this field has parameters’ gradient, the source starts moving toward
the lesser magnitude parameter until it reaches the area of absent gradient.
The source perceives this process as unequal wave pressure around it driving it
to the potential’s hole.

Fig.72
Two sources of
waves are in the nodes of the standing wave they’ve created. The nodes are
areas of stable balance for the sources. In these areas the gradient of the
wave field energy is absent.

Fig.73.
Attempts to
bring the wave sources closer, i.e. to take them out of potential’s holes, lead
to the reaction of the standing wave aimed at bringing the sources apart. The
reaction lasts till the sources are again in the balance areas.

Fig.74
Attempts to
separate the sources, i.e. to forcibly bring them out of the balance area, lead
to the emergence of the in-ward emission field which is seeking to bring the
sources to their nodes.

Fig.75
The farther the wave sources from the potential’s holes
the stronger is the impact of the wave field on them. The field is seeking to
bring the sources to potential’s holes.

Fig.76
One has to exert effort to separate the sources. Which
will take them to areas of unstable balance, i.e. on the crests of not fully
formed standing waves. Beyond this border the sources will experience the
pulling apart forces. At this moment attraction between the sources is replaced
by separation.

Fig.77
Moving away from
the center under the influence of the pulling apart forces, the sources will
soon form another two standing waves and slide into new nodes, i.e. new areas
of stable balance (potential’s holes).

Fig.78
Let’s go on
pulling the sources apart – this would again lead to their unwillingness to
leave the potential holes expressed, as before, in emergence of external wave
field and its resistance to the effort.
That’s how
self-organization process looks in which the minimally possible system consists
of two sources and a wave field between them in the form of the standing wave
anti-nodes. Such system can be called ‘RD-dipole’ (rhythmodynamics dipole).
Rhythmodynamics dipole
is a system of two sources held together by the energy
of the standing wave in the nearest areas of stable balance. RD dipole is the
least possible in nature self-organizing system and presents the simplest model
of a physical body.
Any two coherent
sources are self-organized in the system. The distance between the sources is
set according to the rule
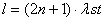 , i.e. there is always uneven number of
standing waves between them. But the sources may be out of phase too.
, i.e. there is always uneven number of
standing waves between them. But the sources may be out of phase too.
Back to contents ↑
§ 3.04 Self-organization and phase displacement
Henceforward we
are to use the term ‘oscillator’ attributing to it the properties of the wave
source.
Let’s examine a
system in which two coherent oscillators are set in the nodes of one standing
wave. Let’s use the notion of ‘phase displacement’. The phase displacement
between oscillators manifests itself in de-synchronization of their
oscillations. If phase displacement is absent, oscillators’ work is
synchronized, i.e. they emit simultaneously the waves of equal in magnitude
amplitudes. Phase displacement implies that waves are emitted with certain
fixed amplitude shift: lead or delay.

Fig.79 In phase oscillators

Fig.80 Out of phase oscillators. Phase
displacement
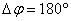
Absence of phase
displacement in the system implies absence of transfer of this system in wave
medium. Phase displacement, on the contrary, makes the system move in the
medium following the rule:
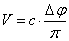 (3.01)
(3.01)
If the system
moves (no outside force is exerted, i.e. supported by the phase displacement)
the distance between oscillators diminishes:
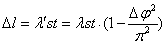 (3.02)
(3.02)
or
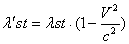 ,
(3.03)
,
(3.03)
i.e. the
distance between oscillators depends on the speed of the system.
Which implies
that with the change of the system’s velocity from zero to V the
oscillators are influenced by the forces of interference nature: in motion, the
standing wave shrinks, the distance between the nodes diminishes, and
oscillators watching the nodes’ position follow in their wake.
Let’s examine
relation of the phase displacement and speed. For the purpose of which we’ll
choose a situation in which a phase displacement was made between the
motionless oscillators (fig.82).

Fig.81. That’s how the system of
oscillators looks (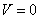 ,
,
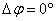 ) in which the parameters of phase displacement
and speed are interrelated according to the rule
) in which the parameters of phase displacement
and speed are interrelated according to the rule
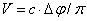

Fig.82 Phase displacement between oscillators
is
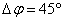
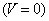 which made the standing wave move right.
which made the standing wave move right.
Relative to oscillators the potential holes shifted
right. The anti-node began exerting influence on the right source trying to
move it toward the diminishing amplitude. On the left source influence is
exerted by the emerging external field moving the oscillator into potential
hole.

Fig.83
When such system
(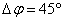 ) acquires a chance of free movement (with
fixed distance between the sources), the system will start moving right with
speed
) acquires a chance of free movement (with
fixed distance between the sources), the system will start moving right with
speed
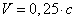 . The distance between the standing wave nodes will
contract according to the rule
. The distance between the standing wave nodes will
contract according to the rule
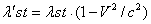 which will lead to difference in position of
oscillators and the nodes. Forces have emerged seeking to place the oscillators
in the moving potential holes.
which will lead to difference in position of
oscillators and the nodes. Forces have emerged seeking to place the oscillators
in the moving potential holes.

Fig.84
If the distance between the oscillators becomes no more
fixed, then, under the influence of external wave forces they are to move to
potential holes, and the distance between the oscillators will equal precisely
the length of the standing wave (fig.84).
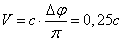
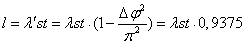
The phase displacement leads to the shift of potential
holes relative to the sources in such a way that the system’s motion with
constant speed becomes its stable condition. Thus, the phase displacement
breaks the inner balance of forces which can be restored only by motion. Such
motion is even and rectilinear, and therefore looks like motion by inertia.
If for any reason the phase displacement between the
oscillators changes, the system’s speed changes too. Evenly increasing phase
displacement would result in speed growth, i.e. the system would self-propel
with acceleration. It must be stressed that it doesn’t matter whether the phase
displacement was caused by some external factor or the system developed some
internal causes.
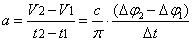 (3.04)
(3.04)
But phase displacement in time means frequency difference
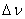 . Having transformed the 3.04 formula we have:
. Having transformed the 3.04 formula we have:
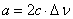 (3.05)
(3.05)
To get the notion with magnitudes of what order we are to
deal with in practice, let’s calculate the frequency difference
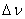 between oscillators when: the system moves with
acceleration
between oscillators when: the system moves with
acceleration
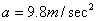 , the speed of waves propagation
, the speed of waves propagation
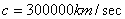 .
.
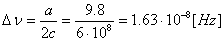
Let’s also
examine the case with absent phase displacement between the sources forcibly
moved to the right with certain constant speed.

Fig.85
 ,
,
 .
.
Deformation of
standing wave develops in such system: it moves left of the sources, and additional
wave field emerges to the right. On the part of the anti-node and the wave
field which emerged to the right the force appears applied to the sources and
preventing the system’s transfer.
To transfer this
system in wave medium is impossible without resistance. The system with no
phase displacement would resist any transfer because it seeks to avoid any
deformations which is possible only with zero velocity relative to medium.
That’s how inertia emerges.
Its
unwillingness to change the motion regime is due to the system’s inability to
change phase relation. The emergence of phase displacement, on the contrary,
would make the system move. As you can see, the speed of transfer and phase displacement
are interrelated parameters:
 ,
(3.06)
,
(3.06)
where
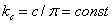
if ñ = 299792458 m/sec. and
ð =180°, then
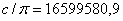 [m/(sec·degree)]
[m/(sec·degree)]
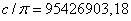 [m/(sec·radian]
[m/(sec·radian]
The correlation of the system’s speed and phase
displacement between the oscillators (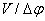 ) is constant and equals the ratio of the
speed of wave propagation in medium to a half-period
(
) is constant and equals the ratio of the
speed of wave propagation in medium to a half-period
(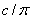 ).
).
If the system resists action aimed at
changing the speed regime, they refer to inertia as a measure of reaction to
action. In the case herein examined the action applied to the system implies an
impulse giving the system additional amount of motion.
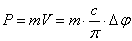 (3.07)
(3.07)
The formula shows that the impulse is proportionate to
the phase displacement, while the ratio
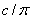 is a sort of coefficient which might be
called a ‘mass quantum’ i.e. with m= 1
is a sort of coefficient which might be
called a ‘mass quantum’ i.e. with m= 1
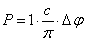 (3.08)
(3.08)
where the the minimally possible mass (mass quantum)
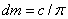 (3.09)
(3.09)
There’s incentive to introduce a notion of ‘rhythmodynamics
mass’
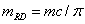 (3.10)
(3.10)
measured in [kg·m(/sec·radian)]
Back to contents ↑
§ 3.05 Kinetic energy
Relation between
speed and phase displacement allows us to take a different look at the ‘kinetic
energy’ notion.
As energy is
attributed with ability to do work, and work is linked with such notion as
‘force’, let’s examine the notion of ‘force’ as well.
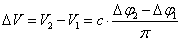 (3.11)
(3.11)
 (3.12)
(3.12)
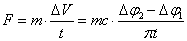 (3.13)
(3.13)
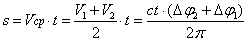 (3.14)
(3.14)
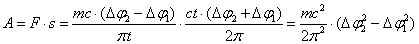
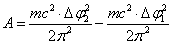 (3.15)
(3.15)
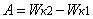 (3.16)
(3.16)
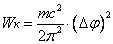 (3.17)
(3.17)
where:
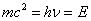
The 3.17 formula differs from the usual (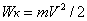 ) in its right part which shows clearly the
gradient-phase nature of kinetic energy (i.e. the inside system processes which
provide this energy). The mass coefficient of proportionality (m) shows
only the number of elementary systems which remains constant with all possible
phase displacements and, consequently, with all velocities matching those
displacements. Mass is a quantitative measure (expressed in ‘things’) of
elementary systems in object and therefore, whatever velocity regime this
object might have, its mass is always constant because the number of oscillators
and systems they form cannot change without a cause.
) in its right part which shows clearly the
gradient-phase nature of kinetic energy (i.e. the inside system processes which
provide this energy). The mass coefficient of proportionality (m) shows
only the number of elementary systems which remains constant with all possible
phase displacements and, consequently, with all velocities matching those
displacements. Mass is a quantitative measure (expressed in ‘things’) of
elementary systems in object and therefore, whatever velocity regime this
object might have, its mass is always constant because the number of oscillators
and systems they form cannot change without a cause.
The presence of phase displacement in 3.17 formula
corresponding to a certain magnitude of speed V indicates the system’s
intention to have precisely this speed. If the free movement is obstructed the
system would exert constant pressure on the obstacle with a certain constant
force. I.e. if this system is restrained its kinetic energy should be regarded
as potential seeking to become kinetic. Such system has inner necessity to
move, and the energy which provides this necessity is called potential.
Potential energy is transformed into kinetic one if the system is no longer
restrained.
Under condition
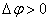 ,
,
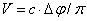 the energy is kinetic
the energy is kinetic
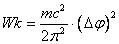 (3.17)
(3.17)
Under condition
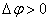 ,
,
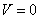 the same energy is potential
the same energy is potential
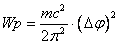 (3.18)
(3.18)
When 3.17 and
classical
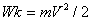 formulas are compared, the latter in no way indicates
the root-cause of energy, whereas the rhythmodynamics approach shows processes
responsible for motion as well as kinetic energy notion. It shows a unified
mechanism of kinetic and potential energies which is essentially the presence
of internal phase displacements. These displacements, in cases when free
movement is obstructed, become manifest in the form of the inner propulsion
force (in the form of propensity to move).
formulas are compared, the latter in no way indicates
the root-cause of energy, whereas the rhythmodynamics approach shows processes
responsible for motion as well as kinetic energy notion. It shows a unified
mechanism of kinetic and potential energies which is essentially the presence
of internal phase displacements. These displacements, in cases when free
movement is obstructed, become manifest in the form of the inner propulsion
force (in the form of propensity to move).
* * *
Now we have a
model notion of the processes responsible both for kinetic and potential energies
as well as motion. Which means one can test experimentally the correctness of
rhythmodynamics approach to the means which provide motion. It’s obvious too
that if wave medium doesn’t exist in real experiment we won’t be able to create
a self-organizing system in space, to say nothing of making it propel by
controlling the phase correlation between the active elements of the system.
Back to contents ↑
§ 3.06 Wave model of elastic object
Simple model and
real experiments show that wave systems have a propensity to form
(self-organize) in space lattice structures, similar to structures of physical
objects.
For the
self-organization to take place and the ties between the sources to acquire
elasticity wave medium is required, as well as oscillating sources and
emergence of standing waves between them.
The sources are
in phase and form a model of artificially elastic body comprising numerous
macroscopic elements positioned at macroscopic distances from each other and
elastically tied together by wave fields. This is the most simple example of a
system which is self-organized in time and space. This object has certain
dimensions, it can move and undergo accelerations as any natural object. The
wave fields and forces uniting the elements into a single object are not deeply
hidden in the micro-world, so we have a chance to objectively examine such
issues as: how and why do the object’s dimensions depend on its speed; how do
the phase displacement and frequency difference trigger object propulsion and
determine its speed.
Let’s start with
the fact that every source (oscillator) reacts only to those changes which
emerge in close proximity. The waves departing from the sources are objects of
their own, i.e. at the moment of their emission and departure from the source
they sever ties with it. Potential’s holes in the form of the standing wave
nodes and areas of unstable balance in the form of the crests of anti-nodes
emerge in interference field.
Stable balance
is a state when after a small alteration of the
object’s position forces emerge in the system seeking to bring the system back
to balance, and the balance is not broken; the body returns to position of
balance while disbalance is not increasing with time.
Unstable balance is a state when after a small alteration
of the object’s position balance is broken, the object does not return to the
position of balance and balance displacement is increasing with time.
If at the moment
of interference field formation the sources are outside potential’s holes, the
interference field drives them into the nearest potential’s holes. During their
transfer the sources continue emitting waves, the interference field is
changing in the wake of the moving sources. This happens with some lag due to the
finite speed of waves in medium. During this lag interval the position of
potential’s holes changes as well.
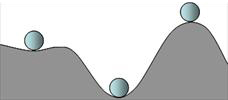
Fig.86 Areas of stable (potential’s
holes) and unstable balance.
A situation emerges
in which several wave sources are seeking to find and occupy the nearest
potential holes in their own constantly changing interference field. This
process can end in formation of a stable system with elastic ties between the
elements, or in disintegration of as yet unformed system.
I wonder if
modern mathematics is able describe the process of the sources’ search of potential
holes, as well as other transformations connected with the self-organization of
numerous wave sources?
Nature is
unaware of the man-made math. What is natural there can be extremely
complicated in mathematics. But there’s other little known way of calculations.
With its help one can describe behavior of numerous sources during their
self-organization. Unfortunately, this method cannot be explained briefly; it
demands special explication.
Suppose,
self-organization took place of an artificial stable object the active elements
of which became set in potential holes. Such object with initially set
parameters (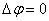 ) develops a problem with motion in wave medium. Potential
holes in which active elements are set are formed by wave fields radiated by
other object’s elements from other positions. The waves are moving with finite
speed, therefore any changes in interference field are not instantaneous, but
delayed. If the artificial object, i.e. all its active elements, were moved,
the potential holes would be moving with some delay, i.e. they would be lagging
behind the elements. The elements would be bumping into those potential
potholes; thus forces emerge which impede progress. There will be no motion by
inertia.
) develops a problem with motion in wave medium. Potential
holes in which active elements are set are formed by wave fields radiated by
other object’s elements from other positions. The waves are moving with finite
speed, therefore any changes in interference field are not instantaneous, but
delayed. If the artificial object, i.e. all its active elements, were moved,
the potential holes would be moving with some delay, i.e. they would be lagging
behind the elements. The elements would be bumping into those potential
potholes; thus forces emerge which impede progress. There will be no motion by
inertia.
Until something
changes, the work of restraining forces won’t stop, and the elements won’t move
in holes and in agreement with them. Until
something changes, the object would be moving as long as external forces are
applied to it; the fields (potential holes) would be always lagging behind the
elements and forces would be active, pulling the elements back to stable
positions.
To prevent these
inhibitory forces from appearing the potential holes must emerge where elements
are expected to be prior their movement. What changes should occur for this to
take place, and how can these changes be organized?
As we already
know there’s relation between velocity of movement and phase displacement. It’s
this phase displacement which can secure the synchronized movement of the
elements and potential holes. In such case the motion in wave medium will
proceed without hindrance. What is needed is a compulsory control over phase
correlations, or self-synchronization of phase relations.
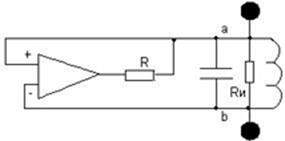
Fig.87 Phenomenon of mutual
synchronization of auto-oscillations is well-known among radio engineers. Those
who do not know this phenomenon can consult a mathematical equation which is
not difficult to record for the simple generator scheme shown on the picture. An electric dipole in the form of two
balls can be connected to the circuit as it’s shown on the picture, the coil
can be screened, and we’ll have Hertz’ oscillator.
Self-organization
would be complete and artificial object closer to natural if oscillations in
the elements were autonomous and also subject to self-synchronization, i.e.
automatic matching in frequency and current phase with other elements.
Such system
could be created by means of radio engineering.
Back to contents ↑
§ 3.07 Properties of artificial elastic bodies
Velocity –
phase displacement dependence
If artificial
object is made on electromagnetic foundation, i.e. its elements are active
resonators, the speed of motion of such object will depend on the phase
displacement between the resonators. Let’s calculate phase displacement needed
to provide the object’s velocity of, say, 1 km/sec.
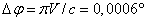
Which doesn’t mean that our artificial object would
immediately tear off the place picking the required speed; the forces of
electromagnetic ties are not so big. But the object would have a propensity of
picking the speed precisely due to the shift of electromagnetic potential holes
ahead of resonators. Here the phase displacement would create a situation in
which potential holes move first, while resonators and the object follow in
their wake as a consequence. The problem of direct experimental testing is that
the open space of cosmos is required where the impact of external forces is
minimal.
The experiment could be also staged in some dense medium,
say, water. Two options are possible there: on surface and underwater. Fig.75
shows experiment on surface with two oscillating floats with controlled phase
displacement.

Fig.88
The experiment’s
goal was to confirm theoretical conclusion about dependence of object’s motion
velocity on phase displacement between its elements. The example of artificial
body proved the correctness of conclusion: phase displacement was created
between the elements of the system which brought it into motion.
In the second
half of 19th century Carl Anton Bjerknes staged an experiment with pulsating
under water drums. Later similar experiments were staged in air which proved
that phase displacement does affect sources behavior.
In the middle of 19th century
Norwegian physicist Carl Anton Bjerknes (1825-1903) proved that two pulsating
balls with radiuses too small in comparison with the distance between them,
being submerged into (non-compressible) liquid, can trigger either attraction
(gravitation) or repulsion (anti-gravity) to each other. The balls were
attracted with a force directly proportional to the product of pulsations’
amplitudes and inversely proportional to the squared distance between their
centers in the case when frequency of pulsations and their phases coincide. If
pulsations’ are in opposite phases attraction is replaced by repulsion. (V.
Bjerknes. Lectures on hydro-dynamical long-distance forces according to
theory of Carl A. Bjerknes, 1990). It should be emphasized that these are
the same bodies but with different frequencies. The fact must be pointed out
that the experiment was staged in practically non-compressible medium, liquid,
i.e. in his experiment Bjerknes dealt not only with ideal conductors of waves
and frequencies, but with objects which were in a state close to
weightlessness.
According to Bjerknes, for attraction, balance or
repulsion to become manifest, pulsation must take effect in the following
cases:
·
pulsation of all
particles must coincide in frequency and phase;
·
intensity of pulsations
should be proportionate to their masses.
The effects of the drawn up hydrodynamics theory of
gravitation at the level of frequency-wave modulation were demonstrated by
Bjerknes in 1861 at Paris electrical exhibition when two pulsating under-water
drums attracted attention of some scientists. In 1885 another scientist Pierre
Leahy found that in a compressible medium the work of two balloons pulsating
with equal frequency and phase changes its character
if
the distance between them exceeds half of wavelength. Therefore to
correctly explain gravitation through Bjerknes’ pulsation one had to assume
‘ether’ of cosmic space as absolutely non-compressible – which was difficult to
imagine, regarding ‘ether’ as some kind of matter.
In 1898 positions of Bjerknes theory became much
stronger after Wilhem Weber found that all pulsating objects have a remarkable
propensity for self-regulation: the forces which excite waves in medium quickly
bring the pulsation of interacting masses to synchronism, even though such
synchronism was absent before. Weber came to conclusion that the structural
elements which made up the matter pulsate due to
their own physical nature, and these pulsations automatically bring about
synchronism, which leads to realization of Bjerknes’ second condition: direct
proportionality of pulsations’ intensity to the
magnitude of masses of pulsating objects. It must be noted that the physical
cause of interaction (gravitational property of additivity) was comprehended at
the level of mechanical notions.
Functionally, the hydrodynamic model of interaction
(gravitation) at the level of frequency-wave processes was a perfect
explanation of all at the time known gravitational effects, bringing them down
from the level of interaction of immeasurably large objects to actually
microscopic level. Moreover, it amply explained not just the nature of
gravitation or balance of interacting bodies, but also predicted possibility of
repulsion, or anti-gravitation, which was unusual and revolutionary in its
ramifications and surpassed the ideas of modern physics.
From these positions by the early 20th
century Bjerknes’ theory could be regarded the leading mechanistic theory of
gravitation (mechanical ideas of Newton still have their grip on modern
physics) which had unquestionable advantages over all other known at the time
interpretations of physical nature of gravitation or interrelations in material
world. Everything tapered down to experimental discovery of ‘ether’, material
with properties which Bjerknes required, in particular, its absolute
non-compressibility. Appropriately, the modern physics of the 20th
century which unequivocally proved absence of any ‘ether’ – naturally, in its
mechanistic interpretation of the notion – dealt a lethal blow to gravitational
hydrodynamics.
There are
analogies in the living world too: to propel in medium microorganisms can use
their own vibrations. There are such among the hydrobionts: noviculae,
oscillaria, pinnularia. Hydrobionts have attracted attention for two reasons:
1) absence of the means of propulsion in their environment 2) the mechanism of
propulsion in their environment is not precisely clear.
Fig.89 Naviculae (left),
oscillatoria (right).
Naviculae is an
organism in the form of a quartz shell with cavities inside filled with live tissue.
The live tissue is supposed to generate electric
potentials which the quartz shell transforms into high-frequency vibrations,
which are transmitted to water in the form of waves. A high-frequency acoustic
interference field with two (according to the number of emitters) potential
holes emerges around naviculae’s body. The emerging phase displacement between
the shell’s ends shifts potential holes relative the emitters which triggers
the noviculae’s propulsion. In other words, it’s a self-propelled organism.
Oscillatoria is
an algae whose parts are self-propelled in its environment (water). Biologists
are not unanimous about the mechanism of oscillatoria’s propulsion. The algae
is thought to excrete a mucus in which it slides.
Object
dimensions depend on velocity
Michelson’s
experiment is still one of the key questions of science. There are several hypotheses
explaining its results, but none of them have a model illustration, nor do they
show precisely how the end result is nullified.
If one knows the
relation between the standing wave length and velocity one can apply this
phenomenon for the standards of measure and condensed objects. One can also create artificial elastic objects in
various mediums to demonstrate dynamics of relation between these objects’
dimensions and velocity. The working model, which has no practical use, is
quite complex to adjust, so we’d better limit ourselves to simulated
experiments and computer modeling.
The distance
between the standing wave nodes depends on velocity. In the artificial object
the nodes play the role of potential holes, i.e. when motion in medium begins
the distance between the holes shrinks and the object’s elements are affected
by the forces of interference nature, which bring these elements together.
Consequently, the object’s dimensions diminish. Such is the mechanism’s cause
of reduction of dimensions of the moving objects.
One cannot
discover directly the reduction of dimensions in Michelson’s experiment because
all bodies and standards of measures change their dimensions synchronously and
proportionately. This is the consequence of internal self-organization of all
bodies in nature.
Back to contents ↑
§ 3.08 Inertia is the property of system
Definition of
inertia: body propensity to resist the impact on it until its elements
capable of self-synchronization enter a new regime of self-synchronicity.
How does it take
place?
At the moment of
the start of motion the active elements of the body shift relative to potential
holes, i.e. potential holes drag behind the elements. Inertia, or resistance to
impact, would continue until the elements’ phases become adjusted to the state
of motion. Which takes time because waves in medium spread with finite speed.
The object has a
‘feel’ of inertia when force is applied not to all object’s elements at once,
but to some of them. If it were applied to all at once as is the case with
gravitation, the feeling of inertia would be absent.
Using the
example of a simple system of oscillators we could describe the process of
inertia formation the following way.
Let’s act on an
oscillator with the aim of moving the system. The oscillator will shift, and
the length of the wave it emits is to change too. The other oscillator in the
system stays in place until it receives a signal from the first oscillator in
the form of the wave which has changed its parameters. The altered wave which
has reached the second oscillator will exert its influence by changing the
position of its potential hole. The oscillator will shift in space and the
waves it will be emitting during this period will be of different length. But
the first oscillator continues resisting the impact on it. When the wave from
the second oscillator comes back to it its potential hole will shift, and
resistance will be over.
Conclusion:
resistance to impact (force of inertia) on the first oscillator will last as
long as it takes to transfer this oscillator and send a signal about the end of
this transfer to the second oscillator and back, i.e.
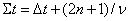 (3.19)
(3.19)
where
 – time of impact on the system
– time of impact on the system
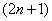 - number of standing waves between the
extreme ends of the system.
- number of standing waves between the
extreme ends of the system.
Back to contents ↑
§ 3.09 Model view on self-propulsion of molecules
Because of their
miniscule dimensions, no one has seen yet either the structure of molecule or
atom. The hypothetical schemes of these formations are built on the basis of
indirect, obtained by instruments, signs which disclose both behavior and
properties of atoms and molecules. One of their properties is self-propulsion.
Let’s examine
the cause of self-propulsion using the example of water molecule (Í2Î).
Under normal conditions one might expect that the bonds of oxygen atom with two
atoms of hydrogen in Í2Î molecule form at the central oxygen atom a very obtuse angle, close
to 180°. Surprisingly enough, this angle happens to be not 180°, but only 104°31'.
Which makes the inner molecular forces not fully compensated and their excess
manifests itself outside the molecule. Brownian motion is thought to be one of
those manifestations.

Fig.90 Brownian motion, random
fluctuations of tiny particles suspended in liquid or gas under the impact of
colliding molecules of environment, was discovered by Robert Brown.
Outwardly, the
molecules which exert their influence on a particle seem to have a
self-propulsion propensity. The motion is characterized by kinetic energy. But
is it Í2Î internal energy? If so, where does it come from
and how is it produced? Besides, can we speak of self-propulsion properties of
a single molecule of water, being isolated from the rest of water molecules?
If
self-propulsion is a forced reaction of the system to the contradictions
between its elements, in this case they can be created and maintained
artificially or can be the consequence of the system’s constructional
peculiarity.
If the elements
of a system are the sources of waves in wave medium, and their elastic ties are
realized by standing waves, then any internal contradictions in the form of
phase displacement and frequency difference violate synchronicity and consequently
make the system liable to move.
Self-propulsion is an inner-motivated involuntary change of the system
which is determined by its contradictions indirectly reflecting the impact of external factors and conditions. The
conception of self-propulsion in dialectic materialism regards inner
causes as the source of self-propulsion. They are, first of all, contradictions
ascribed to all objects with systemic structure, or other forces, for example,
interaction of isolated components of the system. The influence of external
conditions on individual self-propelling system is brought indirectly through
internal sources. Self-propulsion connected with direction, irreversible
changes, presents a special kind of self-propulsion, self-development. On this
issue the concept of Self-propulsion matches the general dialectic
concept of development in which “…the main attention is paid to
studying the source of self-‘propulsion’” (V.Lenin. 5th edition,
volume 29, p.317).
The RD modeling
of Í2Î molecule as a system of active sources
(oscillators) corresponding to two atoms of hydrogen and one atom of oxygen
presumes that interaction of atoms-oscillators of different phase-frequency
parameters is taking place. The combination of those phases and frequencies is
such that emergence of a stable system becomes possible. Hydrogen atoms may be
in phase, their frequency parameters are different from those of oxygen atom.
That’s why building a model we ascribe equal frequencies to H-oscillators, and
a different frequency to O-oscillator, which is proportionate to a distance between
O-oscillator and any of H-oscillators.
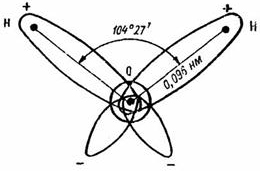
Fig.91 The draft of the water molecule
structure: molecule’s geometry and electrons’ orbits.
If H and O frequencies were equal, in space these atoms
would occupy symmetrical positions.

Fig.92.
Distribution of wave energy in a system of three in phase
sources which are set in potential holes. The energy is localized symmetrically
in the area between the sources.


Fig.93
Phase
displacement between the sources triggers re-distribution of the wave field
energy both inside and outside the system, violation of symmetry in relations
(loss of synchronicity) and development of propensity to motion. The system
with phase displacement has two options: either 1) to eliminate the phase
displacement by auto-adjusting the oscillations of its sources to the
oscillations of the system or 2) to neutralize through motion the internal
tensions which emerged. Both options trigger changes in the system’s motion
regime.
The distance
between oxygen atom and hydrogen atoms in a water molecule is 0,96Å,
while the distance between two hydrogen atoms is 1,5Å. If these distances were considered the standing waves lengths,
then the wave linkage between two atoms of hydrogen is realized at the
frequency of 1,0·1018Hz, while the oxygen-hydrogen linkage has the
frequency of 1,56·1018Hz. To have a visual notion about the wave
field, or rather about distribution of wave energy, one has to process this
data by a special computer program. It produces a picture in which asymmetry is
clearly visible.


Fig.94 RD model of wave energy
distribution in a water molecule.
According to RD model, the distribution of energy in
Í2Î molecule is
always asymmetrical. Synchronicity is violated in its design, and therefore
this violation can be neutralized only through motion.
The model of a water molecule indicates the inherent
asymmetry of energy distribution, and therefore the ‘design’ disbalance of
internal relations between the sources. The water molecule is destined to
self-propel, i.e. self-propulsion is its natural state. What’s important is
that this model allows us to at least have an idea as to why and how, through
what internal contradictions and inconsistencies, such
self-propulsion is implemented.


Fig.95 Model presentations of the energy
distribution in Í2Î molecule
Lots of things
in self-propulsion still remains unclear. The question arises, for example,
how, if self-propulsion were recognized, should the law of preservation of
energy be treated? * The system’s velocity increases
without any visible cause, so where does the energy come from? The simple way
of explaining a sustained motion in the micro-world is a phase displacement, or
frequency difference, i.e. the so-called inherent energy notion is exploited.
But let’s not forget that we are dealing with the model illustration of a
hypothesis.
* In a closed system in which no forces of
friction and resistance exist, the sum of kinetic and potential energy of all
objects in the system remains constant. The full mechanical energy of the
system of objects remains unchanged in the process of their motion if external
and internal forces applied to the system of objects
are potential.
The law of preservation of energy is one of the
fundamental laws according to which the most important characteristic, energy,
is preserved in a closed system. All known processes in nature obey this law.
In a closed system energy can only be transformed from one state to the other,
but its quantity remains the same.
In an open system energy can change with the same parallel
change in the energy level of the objects around the system, or with a change
of energy of system’s interaction with the surrounding objects. The energy
change in the course of the system’s transfer from one state to the other does
not depend on how (by what means and interactions) this transfer is
implemented. The change of energy in the system occurs when work is performed,
or when a certain amount of heat is transformed to the system.
If wave medium
is an element of the system, as RD stipulates, no law is violated there. The
model in question is, on the one hand, open, being inside of unlimited
‘reservoir’ of wave medium, on the other, being the element of a conditionally
closed big system. Moving inside the reservoir the system passes some energy to
it in the form of an impulse, which leads to the preservation of the common
center of mass of the ‘reservoir’ and the system. As the size of the reservoir
and the mass of wave medium are infinite, they can be ignored in calculations.
Even the
existing definitions make one conclude that in the course of water molecule
self-propulsion its potential energy diminishes while kinetic increases, i.e.
the sum of energies remains constant.
* * *
In experiments
with pulsating underwater spheres, on surface fluctuating cups, and with coherent
acoustic emitters, gradients of wave pressure on the sources emerge during the
period of broken synchronicity. The pressure disappears as soon as the sources
again are set in potential holes. Any attempt by the source to leave the
potential hole triggers counter-action in the form of wave pressure.
It becomes
obvious that uniform rectilinear movement of an object as a system is actually
made possible and maintained by the phase displacement between its active
elements. Controlling phase displacement so that
potential holes could be in their motion always ahead the object’s active
elements located in them, we could accomplish a new way of propulsion.
Back to contents ↑
Chapter 4. Motion
Understanding of the cause of motion leads to
understanding of nature!
At present
virtually all fundamental properties of Nature are defined as inherent, inborn,
in other words, the processes on which these properties of Nature are founded
are thought to be beyond human comprehension.
A good point in
question is the critical situation with ether (1881 – 2007), which hasn’t been
solved yet in a consistent comprehensible way, as a result of which the
luminiferous medium has been awkwardly rejected. The situations with the nature
of gravitation, inertia and mass are no less embarrassing – these questions
have been posing problem for over 300 years. As for the nature of motion in
general and transfer of objects in particular, Aristotle tried to answer this
question as far back as 2500 years ago.
It may seem that
the problem of motion (we are referring here only to the transfer of objects in
space) is in principle impossible to solve. But this is not so. At the level of
model presentation the problem of motion was successfully solved as far back as
1996 [7], i.e. in the past millennium. And bearing in mind that any scientific
theory is based on a system of postulates and actually is nothing but a
subjective model of objective reality, the proposed and drafted methods of
rhythmodynamics are in no way worse than any other which exist. The more so
that rhythmodynamics in its potential development is focused on advancement and
use of the new knowledge in solving technological, economic, social,
humanitarian and other problems.
There is a
single universal algorithm, a sequence of rules which reveals not only the
nature of motion, but also manifestations which accompany it:
self-organization, inertia, force. But let’s not forget that rhythmodynamics is
only a model presentation of the things cited, and one must constantly verify
its accuracy by tallying it with natural phenomena.
Let’s examine a
sequence of processes which form and sustain the motion of active elements in
wave medium. I refer to the driving force without which motion (even by
inertia) is impossible.
Back to contents ↑
§ 4.01 Motion as a fundamental property
To illustrate
the problem of understanding the nature of motion in general, and mechanical
motion (transfer) in particular, let’s have a look at the present definitions:
Motion
1. Form of matter existence, continuous process of material world
development. There is no matter without motion, and no motion without matter.
2. Transfer of somebody or something along a definite path. Ex. Rotational
motion. 3. Change in position of a body or its parts. 4. Transfer from one
state, stage of development to the other state, or stage.
If
motion
and matter are inseparable, then to comprehend the essence of motion
it
would be worthwhile to learn what matter is.
Matter -
is a philosophical category which, within the framework of
materialistic philosophy, is the conceptual foundation of science. According to
materialistic dialectics, matter is objective reality, sensually perceived…
Within the
framework of materialism motion was regarded as a form of existence of matter.
Within the framework of modern science motion is regarded in context of its
role in such phenomena as space, time and energy (special and general theories
of relativity). In quantum mechanics, which examines phenomena inside atom as
well as motion of elementary particles, there is a notion of transfer of wave
packages, but it has never been linked to the motion of macro-bodies.
So, science has
no notion of the mechanism of motion, i.e. motion is recognized
as inherent quality which doesn’t need any explanation of its origin (one has
to admit that the root-cause of motion is, indeed, impossible to find).
The mechanical
motion
(transfer) is also regarded inherent quality. When a body moves in space or
relative to other bodies the main cause of its motion is thought to be force
applied to it. As for the question ‘How exactly is the body transfer along a
certain path made possible after the force has been applied to it?’, this
question is generally thought inappropriate because motion (by inertia) is the
usual phenomenon.
The RD models
view motion as a means of solving
contradictions between the qualitative transformation of the object itself and
changes this transformation triggered in environment.
Back to contents ↑
§ 4.02 Translational motion
Translational
motion is one of the forms of mechanical motion of bodies in space. Such motion
can be uniform and accelerated.
Transfer
is a more precise notion which comprises such applied questions as
what’s transferred, where from and where to, in what and relative to what, by
what means and at the expense of what, how fast and in what regime?
Transfer
can be absolute, i.e. proceeding in a reference frame linked with
wave medium, and relative.
To form a model
notion about the processes which take part in organizing the translational
motion let’s repeat the original conditions:
·
Oscillator (wave source) is always seeking to
occupy a stable position in wave medium in which the overall influence on it
from the wave field will be zero. Such place is called potential hole.
·
The motion of potential hole triggers the motion
of the source, and if the source’s motion is impeded, the source exerts force
on the obstacle.
·
If forcible transfer of the source does not
trigger the transfer of potential hole, the source begins resisting the
transfer due to the gradient action of the wave field.
Now let’s
examine a simple wave system with two coherent sources. The distance between
the sources equals one standing wave, while potential holes coincide with the
nodes; the phase displacement between the sources is zero (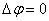 ).
).

Fig.96
Such system
(fig.96) has to reason to move in wave medium because positions of the sources
and potential holes coincide. Here we can talk about the state of absolute rest
characterized by the following parameters:
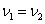 ,
,
 ,
,  ,
,
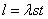 .
.
Let’s call this
state the first state of quiescence.
To create a
situation in which the potential holes are to shift relative to the sources one
has to create a phase displacement between the sources’ oscillations (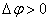 ).
).

Fig.97
Phase
displacement triggers the shift of potential holes relative to their initial
position, and appropriately, the shift of sources. The sources are influenced
by the wave field so their natural reaction would be motion toward potential
holes. If such motion is not obstructed the sources will be moving until they
find themselves in the areas of stable balance.
For the sources
to be again in potential holes with the standing wave anti-node between them,
the system must pick a certain velocity V.

Fig.98
There is a
correlation between the phase displacement, dimensions and system’s velocity, a
correlation of parameters:
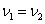 ,
,
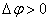 ,
,
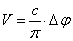 ,
,
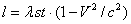 .
.
The system is moving
uniformly, the sources and potential holes occupy the same position, but phase
displacement creates a lively standing wave between the sources. There’s no
basis to speak of internal deformations inside the system because the moving
system is in a state of internal balance. Let’s call this state the second
state quiescence.
The third
state of quiescence is a situation when phase
displacement between the sources’ oscillations changes with time, which makes
the system move with increasing speed, i.e. acceleration. The situation is
remarkable because increase of its own speed triggers no counter-reaction on
the part of the system, in other words it is neutral to it, being in a state of
internal rest. The third state of quiescence can be realized artificially,
and in reality it takes place in a free fall in gravitational field (the field,
in the same way as was described, changes phase and frequency parameters of
body elements).
Let’s give the
usual examples of phase interpretation of motion.
Example 1.
Two men in a boat are going to throw two stones of equal mass in
opposite directions. If they are to throw them simultaneously the boat will
remain still. But what is to happen, on condition friction between the boat and
water is absent, if stones are thrown one at a time?

Fig.99 Illustration of example
In a space of
time between the throws the boat will shift, say, by 100 meters. Will the boat return to its initial position after the second throw? No,
it won’t; it will stop. If this procedure is repeated, the boat will move
another 100 meters despite the fact that equal amount of stones
(matter) has been thrown in both directions! And suppose such process were
sufficiently prolonged and had wave nature, i.e. were invisible and proceeded
without the loss of mass? Won’t the boat motion seem a miracle in such case?
In this example
the boat transfer is linked with specific processes which have a
phase-frequency component. It’s these processes which brought about transition
without any outside action.
Example 2
Ivanov-Didin experiment.

Fig.100. System’s motion in medium brought about by
phase displacement between the sources’ oscillations.
In both
experiments, the first hypothetical and second real, motion is implemented
through phase displacement between active elements of the system.
Example 3
Fig.101 A microorganism called naviculae moves in its
environment (water) through out-of-phase oscillations of its own quartz shell.
The average length of naviculae’s body is 50 micrometers. Assuming that the
length of the standing wave equals the length of naviculae’s body, then, using the
magnitude of the speed of sound in water (1500 m/sec.) one can calculate the
frequency generated by naviculae: about 15 mHz.
Conclusion:
Motion is not necessarily started by some outside action, external force. There
is another way found which doesn’t need such action:
The system
of sources is moving in medium evenly and rectilinearly when certain facilitating
relations have emerged between the active elements of the system and the
medium; they are characterized by phase displacement and changes in the medium.
Changes in the medium and constant phase displacement between the elements of
the system (body) are not simply participating in formation of a uniform
motion, they are also sustaining it.
Here’s a reverse
order of phenomena participating in formation of conditions and implementation
of transfer: sources motion → wave pressure on sources → potential
holes shift relative to sources → phase displacement between the sources.
The cause of the motion of the system’s elements here is the wave pressure brought
on them which emerges due to the shift of potential holes which takes place
because of the phase displacement between the elements.
With such
approach the phase displacement is the root-cause which triggers such changes
in relations between the elements of the system and wave medium which make the
system move in this medium. The system’s motion is the consequence, or reaction
to the changes which took place in its relations with the medium.
One should
specifically stress that wave field linking the elements is an inseparable part
of the system, therefore any changes in the wave field inevitably lead to
reaction to those changes both on the part of the elements and the system as a
whole.
Aristotle’s
words come to mind in this connection “… the celestial matter (bodies) has a
propensity to restore force which it needs to sustain the steadiness of
motion”.
In the case of
the described model it’s the phase displacement between the system’s elements which
makes such propensity ‘to restore force’ possible. According to RD, there is no
motion by inertia, but there’s illusion of it. The motion by inertia is
maintained by the presence of phase displacement, proceeds with constant speed
and in a state of inner quiescence (synchronicity). If phase displacement is
eliminated (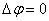 ), the motion
stops.
), the motion
stops.
To implement
sustained motion it is necessary that the speed and direction of transfer of active
elements and potential holes should always coincide. For which one should
ensure synchronicity (resonance) between the system’s motion, phase displacement
of its elements and change in the wave field linking those elements.
Achievement of synchronicity (resonance) in a simple system of sources with
phase displacement between them is possible only if it moves according to the
rule:
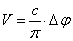 . (4.01)
. (4.01)
When these
conditions are not observed synchronicity is violated. Seeking to restore it,
the system starts moving.
Back to contents ↑
§ 4.03 The nature of the moving force
Much has been
spoken about the motion of bodies by inertia, but no one has indicated yet the
cause which makes such motion possible. And such cause must exist: otherwise
any motion may be regarded as almost a miracle. In which case motion should be
referred to not as a physical process but as a God-given mystery. For example,
Descartes thought that motion of bodies is always triggered by a push given to
those bodies by other bodies. While the general cause of motion in his concept
is God who created matter jointly with motion and quiescence and who preserves
them. Aristotle had a different approach to motion: “A rectilinear motion is
implemented through the elements’ seeking their ‘natural places’”.


Fig.102
We got used to
the idea that all uniform rectilinear motion starts with initial push, and afterwards
is sustained by inertia. But inertia is a quality inherent in bodies, i.e.
being the cause of any translational motion it, nonetheless, requires no
explanation. Whereas we are interested in the root-cause of inertia thanks to
which the body doesn’t stop after the push but keeps moving. In other words,
there must be specific processes which sustain the body’s motion making it
uniform and rectilinear. If such processes exist in nature, they are the
driving force.
The driving
force is usually linked with a difference of something. The usual analysis of
the body’s motion by inertia does not reveal such difference. Of course, the
researchers were not inclined to look for a driving force in what was initially
and traditionally thought as inherent property.
The analysis of
uniform and rectilinear motion of the system of sources (oscillators) in which
the driving force is created and explained by the presence of phase
displacement between the elements reveals a chain of processes: phase
displacement between the elements leads to asynchronicity → propensity to
shift and actual shift of potential holes in motion’s direction → motion
of elements in the wake of potential holes until the speed is reached when
synchronicity is restored. Here the rectilinear motion of artificial body
(system) is implemented through its elements’ seeking their ‘natural places’,
i.e. displaced potential holes.
Aristotle seemed
to know what he was talking about! Now we know too!
So, the nature
of the driving force which is hidden behind the notion ‘motion by inertia’ and
which ensures motion without resistance has now become clear, at least in its
model presentation. But the question rises: by what notions and what parameters
should this driving force be formally presented?
In classical
mechanics they use a tested and viable notion, the quantity of motion. Let’s
use this notion for a formal and qualitative-quantitative presentation of the
driving force:
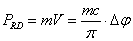 .
(4.02)
.
(4.02)
Unlike classical
mechanics in which the quantity of motion is relative, i.e. depends on the
choice of reference frame, in rhythmodynamics the quantity of motion is
absolute because all body motions are taking place in a medium.
Rhythmus:
A question of practical applicability: is it
possible, using real equipment, to show that the driving force is, indeed, the
consequence of phase displacement among active elements of the system?
Dynamicus:
If such device were technically possible it would
present a ‘simple’ way of almost direct transformation of electrical energy
into translational motion. But I’m afraid at first the would-be machine might
be compared to the first computer, being as bulky and ineffective.
Back to contents ↑
§ 4.04 Three states of quiescence
We’ve mentioned
three regimes of motion in space during which the moving objects experience no
internal tension and matched them with three states of quiescence. For
internal observer, his senses, these states of quiescence do not differ from
each other, therefore it’s difficult for him to judge in what speed regime the
moving system (body) is.
We are used to
the idea that the change of speed regime inevitably manifests itself in the
form of body reaction to the performed action. Speaking in the language of states
of quiescence, during external action the balance of internal forces is broken
and the body reacts by resisting.
Let’s imagine a
hypothetical situation in which the change of speed regime has no bearing on
the state of inner quiescence.
Here’s an
example. The object under study is situated at a certain fixed distance from
the source of gravitational field. Suppose, this field is absent, i.e. not
emitted (switched off). There are no forces between the source of the field and
the object ( ), therefore the object,
relative to the source, is in a state of stillness (
), therefore the object,
relative to the source, is in a state of stillness ( ),
which corresponds to the first state of quiescence.
),
which corresponds to the first state of quiescence.
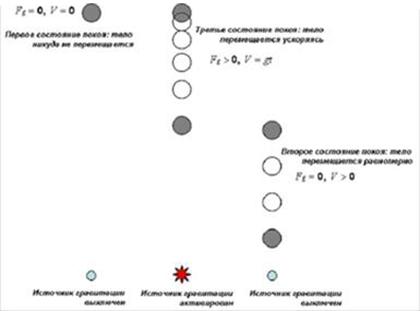
Fig.103
When the source
is activated (switched on), the object under the impact of field (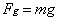 ) starts moving with increasing speed (
) starts moving with increasing speed (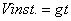 )
toward the source of the field without any resistance, i.e. as if it felt no
force applied to it. This is the situation of the third state of quiescence.
)
toward the source of the field without any resistance, i.e. as if it felt no
force applied to it. This is the situation of the third state of quiescence.
When the object
picks some speed
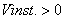 , gravitational field
is switched off and the object is no longer influenced (
, gravitational field
is switched off and the object is no longer influenced (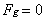 ). The moment the field is switched off the speed regime is switched
from accelerated motion to motion by inertia with constant speed (
). The moment the field is switched off the speed regime is switched
from accelerated motion to motion by inertia with constant speed (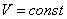 ). The third state of quiescence is transformed into second one.
). The third state of quiescence is transformed into second one.
Obviously all
three states are different in their physical essence, but if judged by
observers’ sensual perceptions or readings of instruments these states do not
differ from each other. So the question arises: is it possible to tell these
states apart without going beyond the limitations of the system, and will this
moment of transfer from one speed regime to the other be felt?
Rhythmus:
Here you are again, especially after your decision to
cancel the law of inertia. Science knows no situations in which action would
not be countered by reaction. Though I may have misunderstood you and something
different was meant instead, so could you explain yourself?
Dynamicus:
The body’s inertialess properties become manifest in
the case when acceleration of the body exists, but reaction to this acceleration
is absent! For example, we are falling in the elevator with acceleration, but
we do not feel the action of force. If gravitational force should suddenly
disappear, we wouldn’t even notice it, nor have it registered by our
instruments, but at the same time our speed regime would change from
accelerated to uniform motion. Moral: we should search more closely because
Nature hides a lot, but few can see it…
Back to contents ↑
§ 4.05 First state of quiescence
Let’s examine
this issue more closely. The system of immobile in medium coherent in-phase
oscillators creates interference field in the areas of stable balance of which
the oscillators occupy their position. Let’s choose the system of two
oscillators as an example.
Fig.104 Analogy of Bjerknes’ experiment.
Two spherical
oscillators (wave sources) are suspended on threads from a boat floating in a
pool. The oscillators are controlled by an operator who can adjust their
frequencies and create phase displacement between them.

Fig.105 If the sources’ frequency were increased or
decreased synchronously the distance between them would decrease or increase
too. Which is due to the fact that the sources are seeking to occupy positions
of stable balance (potential holes) which are located in the standing waves’
nodes.
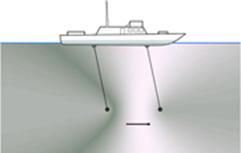
Fig.106 Absence of phase displacement between
oscillators is crucial for the implementation of the first state of quiescence.
Phase displacement leads to deformation of the interference field, and to the
shift of potential holes relative to the sources. The system looses its equilibrium
and acquires propensity to move. The non-equilibrium is compensated by motion.
Back to contents ↑
§ 4.06 Second state of quiescence
If oscillators,
with phase displacement between them, were restrained from motion, the phase
displacement would trigger deformation of the wave field and shifting of the
nodes relative to oscillators.



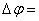 0°
0°
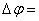 20°
20°
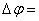 60°
60°
Fig.107 The greater phase displacement is, the greater
is the relative shift of oscillators and nodes.
The nodes
(potential holes) depart from the oscillators, while the changed wave field
exerts force making the oscillators move in the nodes’ wake. When restraining
factor is removed the oscillators will be pushed by the field into potential
holes, and the system will start moving. But, with fixed phase displacement,
what speed should the system have so that position of oscillators and nodes
were the same?
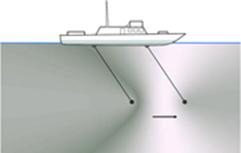
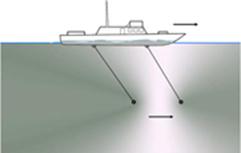
à)
b)
Fig.108 a) If the boat is restrained, force will be
applied to it on the part of the system of the out of phase oscillators; b) if
the boat is not restrained, under the influence of this force it will start
moving with acceleration until it reaches certain speed.
Fig.109 This is how idealized situation looks
(friction in medium is absent) in which the boat’s speed equals the speed of
the moving oscillators and nodes.
Let’s solve the
problem, starting with the analysis of the state of the field in the area
between the oscillators, and find conditions in which coincidence of the moving
sources and standing wave nodes is fulfilled.
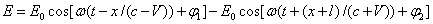
where
l –
distance between the sources
A general case
solution:
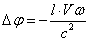 ,
,
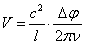 (4.03)
(4.03)
Solution in the
case examined, where
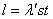 :
:
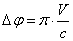 ,
,
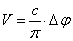 (4.04)
(4.04)
Let’s solve a
reverse problem:
Suppose, we
had two coherent with adjustable phases sources of electromagnetic waves between
which electromagnetic standing wave emerged. What phase displacement between
the sources should be for them to move with speed 8 km/sec. and 100 km/sec.,
and have at the same time their position coincide with the nodes?
We have:
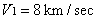 ;
;
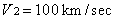
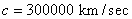 ,
,
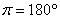
We are to
determine:
 ;
;
Solution:
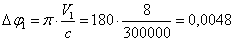
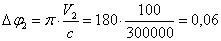
Answer:
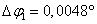 ;
;

How much
these values differ? You can see the illustration below.


Fig.110 The upper picture shows no phase displacement (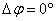 ), the lower picture shows
), the lower picture shows
 which corresponds to the system’s speed
which corresponds to the system’s speed
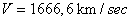 . A naked eye can hardly see the difference between
them.
. A naked eye can hardly see the difference between
them.
Back to contents ↑
§ 4.07 Third state of quiescence
Third state of
quiescence is realized during a free fall under the influence of gravitational
field. It’s the only case when the acting force gives body acceleration while
the body does not react with inertia. How is it possible? Is there actually
some external force which makes bodies fall with acceleration?
If the free fall
were viewed as one of the regimes of motion in wave medium, then the following
relation between the system’s acceleration and the phase displacement changing
in time could be applied:
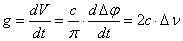 (4.05)
(4.05)
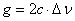 (4.06)
(4.06)
The distance
between the sources of the falling system is changed according to the rule:
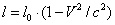 .
.


Fig.111 If frequency discordant system is restrained a
spider-like interference pattern emerges. That’s why this phenomenon is called
a ‘spider-effect’.
Gravitational
field exerts influence on atoms’ frequency parameters, which (frequency discordance)
explains the cause of free fall. Frequency discordance triggers deformation of
internal connections which is followed by the body’s reaction in the form of
self-propulsion with acceleration. If frequency discordance were absent,
reaction to gravitational field would be absent too.
Back to contents ↑
§ 4.08 Specifics of RD modeling
Assumptions and
consequences:
·
Each atom can be imagined as a pulsating
oscillator of some frequency.
·
In solid bodies moving in wave medium the number
of standing wave anti-nodes between the atoms of crystal lattice is always
constant.
·
When body moves in wave medium the standing
waves compress which triggers reduction of interatomic distance and
consequently body dimensions.
·
To explain the effects of gravitation, motion,
etc. a notion of phase displacement
 between oscillators is introduced.
Introduction of a gradient in the form of phase
displacements makes it possible to explain motion, gravitation, inertia, interaction
and other physical phenomena.
between oscillators is introduced.
Introduction of a gradient in the form of phase
displacements makes it possible to explain motion, gravitation, inertia, interaction
and other physical phenomena.
·
Controlling phase displacement one can control
the speed of motion and modify gravitation (including its total neutralization).
Back to contents ↑
Chapter 5. Force, gravitation
|
 |
We know only
one universal force interaction between bodies – gravitation. The bodies react
to gravitational field by moving in its source direction. But the immediate
cause of emerging motion is not the field’s presence but changes which are
taking place in the bodies under its impact.
|
Rhythmus:
I didn’t get you… Explain, please, how can
gravitational field be not the cause? What’s the cause then?
Dynamicus:
We are talking about the cause of mutual motion which
we call ‘interaction’, but we are not talking about the root-cause, the cause
of all causes. Here’s example from our every-day life: a man became
hospitalized with multiple fractures sustained in the road accident of which he
was the cause as he’d jumped the lights. But what was the cause of this traffic
violation? He just learned that his wife had not been loyal to him and became
outraged. But this is not the ultimate cause either. Because two years before
the man had committed adultery and badly humiliated his wife. But this is not
the ultimate cause either…So what ultimate cause of the road accident do you
think the court would examine?
Modern science
regards gravitation mainly as curvature of space which can be presented as a
model. The weak link of such notion is absence of understanding what exactly
curves and why? The question of straightening space and thereby eliminating
reaction of bodies to curvature, which is actually antigravitation, remains
unanswered. No one knows how to do this, that’s why many researchers think
antigravitation impossible.


Fig.112 a) Heavy ball in the center curves the fabric
stretched on the hoop, thus creating conditions for smaller balls’ motion
toward the center of curvature. b) Massive body curves space so that smaller bodies
there ‘slide down’ into gravitational potential hole. ‘Sliding down’ is thought
the natural reaction to curvature gradient.
Science has so
far regarded any physical field (gravitational including) as a special form
of matter, which is in a special state. But the essence of this special
form of matter is unclear, so how can we talk about the cause of
gravitation? Won’t it be more logical to clarify first what exactly changes in
bodies under the influence of this special form of matter , what parameters
change and how, then clarify what the field is and why body parameters change
the way they do? In such case we would be talking about the mechanism cause of
bodies’ reaction through motion, i.e. about processes which ensure this reaction
in gravitational field.
The RD is
talking about the cause of the body’s accelerated motion toward the Earth, not
about gravitational field and its essence. The field’s essence and the way it
influences parameters is the next stage of research. Whereas the cause of the fall
is the discordance of phases and frequencies as if no field existed and this
discordance had no cause, say it were inherent or created and maintained
artificially. What remains is to define the
mechanism of formation of this very motion. Which is quite simple: frequency
discordance leads to potential holes shift and the sources’ drifting in the
wake of those holes until synchronicity regime sets in.
Although lots of
things remain unclear about gravitational field, its presence, no doubt, creates
the force of attraction. Of course, such explanation is inadequate. Let’s
recollect the situation with magnetic field when the field exerts strong impact
on magnetic materials, and none on dielectric materials. Conclusion is obvious:
the correlation of certain parameters in the body made of magnetic materials
changes (is violated) so that this body starts reacting to these changes by
motion, whereas the dielectric body is neutral to the field, i.e. the field
failed to change those parameters. So, what’s important here is the effect of
the field impact which manifests itself in the form of motion.
Back to contents ↑
§ 5.01 Nature of force
The processes
which take part in formation of the notion ‘force’ have been described earlier,
so some overlap is inevitable.
The majority of
our contemporaries have no clear-cut view, nor the answer to the question as to
what the nature of force is.
We’ll be guided
by definitions:
Force
is the essence of action, but not the action itself.
Force
is the cause of the change of body’s velocity.
In
rhythmodynamics force is the consequence of the phase displacement and
frequency difference. The change of these parameters breaks the balance in the
system of elements. And the system doesn’t care whether these phase and
frequency correlations have changed due to internal causes or have been
affected by some outside factor. It’s entirely different approach in which force
which changes the body’s speed has the form of phase and frequency difference.
Whereas the cause of the force as action lies in the system’s elements seeking
to eliminate the emerging rift with their own potential holes. This rift is
eliminated by wave pressure on the elements directed toward the shifting
potential holes. In short, the force of motion emerges inside the body. If the
elements have a possibility of free movement toward the shifted potential holes
the system moves. If the system is restrained, the blockage comes under the
influence of force. When phase displacement changes the amount of effort
on the blockage changes too. One might find this description somewhat
protracted, but it’s precise.
Rhythmus: What you mean is that the root-cause of motion and
force lies in a simple phase displacement? But this displacement too must be
realized somehow; some kind of action is required to effect it, an outside
action too. Which means that the nature of force lies much deeper…
Dynamicus:
You are right, this sequence of cause-and-effect is
endless in nature. So we refer only to the closest cause, as if we were examining
everything in reverse order: action result → action itself → cause
of action → the cause of cause → etc. For example, you get into a
car, turn ignition key, press accelerator – the car starts. Can you name the
precise cause of the car movement here? Whatever the cause is chosen it will
always be the effect of something. Another matter is when you are using model
presentation of a phenomenon which has no in-depth infinity because everything
has been already stipulated in a precise manner.
Resistance to
speed change or counter-force to blockage emerge if correspondence between the
phase displacement and speed regime is not achieved, or it’s broken. If the
system’s speed (acceleration) is higher than what the phase displacement
(frequency difference) allows, we are witnessing resistance to movement. If the
speed is behind the phase displacement (and acceleration is less then what
frequency difference stipulates) a driving force emerges aimed at eliminating
the lag. In both cases we are dealing with internal force which is applied to
achieve synchronicity between the system’s parameters and the processes in wave
medium.
Fig.113 The falling in gravitational field system
seeks to compensate the lack of speed (acceleration)
by
force; and resists when speed (acceleration) is excessive.
The RD
definition of the ‘driving force’ notion:
Driving force is the name of those changes inside the body which make it seek
motion, and sustain continuity of this motion without any outside
participation.
It was noted
before that amount of motion is the measure of such force. Unlike classics
case, rhythmodynamics regards amount of motion as absolute value.
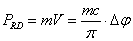 (5.01)
(5.01)
If the system
accelerates we are speaking about increase of its amount of motion and link
this to the increasing in time phase displacement.
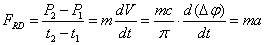 (5.02)
(5.02)
The driving
force is an aggregate of concrete processes which either lead to motion and preservation
of its continuity, or to action applied to blockage.
For a system
which has a phase displacement the driving force is internal; for the blockage
which the system is trying to overcome by its effort the driving force is
external.
Back to contents ↑
§ 5.02 Motion in gravitational field
Depending on the
free motion regime, one can judge the processes which ensure this motion.
In gravitational
field the unrestrained bodies fall with acceleration. Gravitational field is
the cause of this conduct. But its impact is indirect, it only provokes the bodies
by changing then, triggering a chain of events leading to the fact of the free
fall. Let’s examine the cause-and-effect sequence of events in their reverse
order:
Accelerated
motion (fall) → wave pressure on the system’s elements → shift of
potential holes relative to the system’s elements → phase displacement
between the system elements growing in time → gradient density (tension)
of gravitational field → gravitational field → the source of
gravitational field.
Assuming that
gravitational field has a wave nature, i.e. results from aggregation of wave
emissions of all elements of a massive body, we might explain the cause of this
field’s influence on phase and frequency parameters of other bodies. The cause
is well-known: frequency pulling.
Obviously the first observation and
description of synchronization phenomenon of oscillating objects was carried
out by Christiaan Huygens who discovered as far back as the first half of 17th
century that a couple of out of phase pendulum clocks became synchronized when
mounted on a light beam, instead of the wall.
By the end of 19th century John W. Rayleigh observed that two organ pipes with vents nearby start
sounding in unison, if closely tuned, i.e. mutual synchronization of vibrations
takes place. Sometimes the pipes make each other almost ‘silent’. He observed
similar phenomena in the case of two electric or mechanic tonometers linked
with each other. By the end of the 19th, early 20th
centuries synchronization in electric circuits and some electromechanical
systems was discovered.
One of the most amazing phenomena of the examined type
is self-synchronization of unbalanced rotors (rotors the axis of which doesn’t
pass through the center of mass). Two or more rotors which are not linked with
each other kinematically or electrically if mounted on a common movable support
and powered by independent asynchronous motors happen to rotate synchronously
– with equal or divisible average angular velocity and with definite mutual
phases. Rotors’ synchronicity emerges even despite difference between their
partial angular velocities, i.e. those velocities with which they rotate when
mounted on immovable support. (fig.114). The inclination to synchronous
rotation in many cases is so strong that even switching off of one or several
motors doesn’t break synchronicity: the powerless rotors can rotate endlessly.
The energy required to maintain their rotation is supplied by the working
motors thanks to the vibrating support on which the rotors are mounted. This
vibration can be hardly noticeable so observer V might imagine that these
rotors are linked somehow.
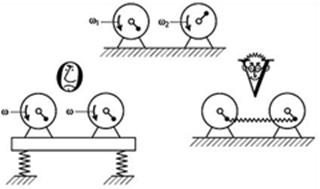
Fig.114 Self-synchronization of mechanical
vibration exciters. Two or more unbalanced rotors powered by asynchronous
motors on unmovable support have different rotation velocities
w1
and w2 (à). If mounted on common movable support
they rotate with equal general velocity w (b). Synchronicity may be preserved
even if one of the motors is switched off (w1=0 or
w2=0). Observer V may have an illusion that
rotors are linked by a spring (c).
Analogy with
vibration mechanics is apparent with the only modification that in rhythmodynamics
wave sources have common movable, floating in wave medium foundation in the
form of a standing wave which ensures the sources’ dynamic link through the wave
medium itself. If this foundation (standing wave) shifts for some reason, the
sources ‘mounted’ on it shift as well. This process may have a different
description: if foundation, i.e. the standing wave linking the sources,
cannot ensure synchronicity between the sources a driving force emerges
shifting the foundation to such speed regime in which there won’t be any need
to eliminate the phase displacement between the sources.
The same happens
in the central gravitational field: the field
imposes the phase displacement and thus breaks synchronicity of the system →
foundation (standing wave) moves and ‘drags’ in its wake the sources →
the trend to speed increase is due to phase shift increasing in time which is
manifest until velocity is reached at which synchronicity of the system’s
sources is possible. If the system is restrained from motion the standing wave
passes efforts from a source to a source aimed at reaching synchronicity.
Synchronicity is
possible either in the absence of phase displacement or in motion. But the
phase displacement is firmly secured by gravitational field which prevents
nullification of the phase shift. As a result, the system is seeking
synchronicity in motion.
One should
distinguish motion-inspired synchronicity from synchronicity in a state of
rest. The synchronicity of a motionless system is characterized by absence of
phase shift; in a moving system synchronicity is characterized by the system’s
motion thanks to which, according to Doppler’s effect, the sources have an
illusion of absent phase shift, i.e. phase displacement is masked by motion. In
both cases there’s no energy flow between the system’s elements, i.e. relative
to its own energy carcass the system is in a state of inner balance which is
the main condition of synchronicity. In other words, synchronicity is realized
because the speed and direction of energy flow between the elements coincides
with the speed and direction of the system.
An outward sign
of broken synchronicity is emergence of outward emission. With absent phase
displacement emission is practically absent (unless it’s uniform radiating in
all directions), with emerging phase displacement emission emerges or changes
the configuration of its distribution in space.


Fig.115 a) Oscillators (2-dimensional model) became
self-organized in such fashion that a standing wave emerged inside, while
outward emission is rapidly diminishing. Synchronicity as a sign of system
stability has emerged. b) Emergence of phase displacement leads to shifting
anti-node of the standing wave and to broken synchronicity. Restoration of
synchronicity is possible only in motion. The system of oscillators will seek
to catch up with the shifting potential hole.
The force of
gravitation is a complex phenomenon which triggers in bodies violation of inner
balance (asynchronicity) and leads to accelerated motion. The changes in body
which participate in formation of the free fall in essence do not differ from
the processes which form any other motion.
The motion in
gravitational field is determined by phase displacement, and as potential holes
in the system tend to be always ahead of the elements which created them, these
elements are forced to constantly increase their speed so as to catch up with
the runaway potential holes.



a
b
c
Fig.116 In gravitational field relative to
the restrained system of wave sources, potential holes are shifted toward the
field source (a). If restraining factor is removed the system starts moving
because the sources will be seeking to catch up with the shifting nodes (b).
Free fall in gravitational field is characterized by absence of internal deformations
in the system (c).
There is only one way to cancel gravitation effect: to
bring the phase displacement between the body elements to zero. Then the cause
which makes the body react in gravitation field will disappear. But to keep
phases in the necessary regime energy may possibly be required.
Back to contents ↑
§ 5.03 Equation to calculate acceleration in
gravitational field
There are
several ways to calculate the formula describing the mechanism of the bodies’
free fall in gravitational field. Here’s one the most curious of them stemming
from familiar premises.
Phenomenon of
gravitational red shift was predicted by Einstein. In earth conditions such
shift is extremely small, nonetheless they managed to measure it with the help
of Mossbauer effect

Fig.117 Shift of fringes, specifically of line A,
toward red.
If photon with
frequency  is emitted at the
height H above the Earth toward the earth’s center, at the level of the
earth’s surface its kinetic energy
is emitted at the
height H above the Earth toward the earth’s center, at the level of the
earth’s surface its kinetic energy
 increases
at the expense of potential energy loss. According to the law of energy
preservation:
increases
at the expense of potential energy loss. According to the law of energy
preservation:
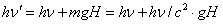 (5.03)
(5.03)
We assume that
photon’s mass 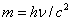 is constant. So,
when photon reaches the receiver with frequency
is constant. So,
when photon reaches the receiver with frequency
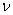 ,
which is different from the one it had when emitted by the source, and with H=
10 m
,
which is different from the one it had when emitted by the source, and with H=
10 m
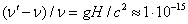

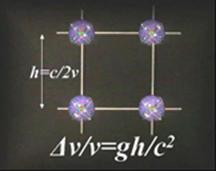
Fig.118
But what will be
the phase displacement of atoms in the gravitational field of the Earth if we
have a crystal of similar atoms in which interatomic distance along the
crystal’s vertical axis is determined by one standing wave anti-node, i.e.
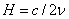 ?
?
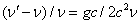 (5.04)
(5.04)
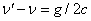 (5.05)
(5.05)
We’ll rewrite
formula 5.05 relative to acceleration g:
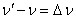 (5.06)
(5.06)
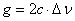 [m/ñ2] (5.07)
[m/ñ2] (5.07)
Now we can
determine what phase displacement between the body’s neighboring atoms should
be for specific acceleration in gravitational field.
With
g = 9,81m/sec2,
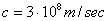 ,
,
then
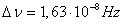
Conclusion: The body reacts by motion to broken synchronicity in
interatomic ties because in motion the body can restore synchronicity. That’s
why during a free fall the body is not in a state of discomfort but in inner quiescence.
Rhythmus: So what’s curious about it?
Dynamicus: This conclusion could have been made long before
rhythmodynamics’ emergence.
Back to contents ↑
§ 5.04 Force of gravitation
According to
classical mechanics, in gravitational field the body m is influenced by
force
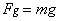 (5.08)
(5.08)
Rhythmodynamics
defines force through discordance of interatomic processes:
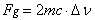 [kg·m/señ2] (5.09)
[kg·m/señ2] (5.09)
where:
m
is a mass ratio of proportionality, quantitative measure of wave
links in body’s crystal lattice [kg];
 is a
frequency gradient in the system of two atoms linked to each other by a
standing wave;
is a
frequency gradient in the system of two atoms linked to each other by a
standing wave;
ñ is
a velocity of light.
According to
5.09,  if frequency
difference is artificially eliminated at the atomic level of matter
organization (
if frequency
difference is artificially eliminated at the atomic level of matter
organization ( ). This conclusion is
particularly important as it helps understand not only at the model level
what’s to be changed in the bodies so as to reach antigravitational effects.
). This conclusion is
particularly important as it helps understand not only at the model level
what’s to be changed in the bodies so as to reach antigravitational effects.
Back to contents ↑
§ 5.05 Comparing formulas
Let’s compare
5.09 formula with the formula of classical mechanics
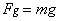 (5.08)
(5.08)
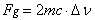 (5.09)
(5.09)
Formula 5.08 reflects
relation between three parameters. It doesn’t reveal the cause of the force,
i.e. there’s no indication of the processes which form accelerated motion (free
fall) of a small body toward the big one.
Formula 5.09
indicates the process which forms the driving force in bodies (gravitational
force) and ensures their free fall.
Back to contents ↑
§ 5.06 Gravitation and frequency pulling
(hypothesis)
What will the
consequences be if phenomenon of frequency pulling is laid at the foundation of
explanation of gravitation?
Frequency
pulling is effective only in the case when interacting sources have close
frequencies. If the sources’ frequency difference is sufficiently large,
there’s no frequency pulling in its pure form. Which implies that the sources’
interaction would depend on the frequency difference between them. Frequency
pulling is possible only until a certain frequency difference after which a
break happens and the system enters a different regime.
There is a known relation
(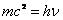 ) according to
which frequency and mass are interrelated. Although the general line of the
idea is correct, there are lots of questions about this relation, for example:
it refers to the mass and frequency of what, of what state and level of matter
organization? We won’t go into details, but we’ll agree that increasing mass of
one of the interacting bodies will change its overall frequency parameter.
) according to
which frequency and mass are interrelated. Although the general line of the
idea is correct, there are lots of questions about this relation, for example:
it refers to the mass and frequency of what, of what state and level of matter
organization? We won’t go into details, but we’ll agree that increasing mass of
one of the interacting bodies will change its overall frequency parameter.
An interesting
picture emerges: gravitational field force based on frequency pulling will increase
until a certain limit after which the increase of mass of big body leads to a
break of pulling. What happens then is not known. Will the big and small bodies
interact gravitationally? But between big bodies of similar mass gravitation
will remain due to proximity of their frequency characteristics. Let’s examine
the situation using the hypothetical black holes example.
Suppose the
black hole increased its mass so that frequency pulling break occurred between
it and ordinary bodies. Suppose gravitational interaction has ceased after such
break, i.e. for ordinary bodies the black hole has become gravitationally safe.
If there’s another black hole of similar mass, frequency pulling will take
place, and these objects will be gravitationally linked. To outside observer a
picture emerges in which the black holes are interacting gravitationally, at
the same time ordinary bodies do not react to the black holes’ proximity in any
way. One might cite the analogy of magnetic field which has no impact on
dielectrics.
A black hole
‘saturation effect’ is present in this situation when its mass increases until
a certain limit after which for ordinary bodies the gravitational properties of
the black hole switch into a new non-gravitational quality. If so, a strong
suspicion emerges that gravitational, magnetic and electrical fields are
identical in their mechanism essence, and their properties reflect only
different frequency bands.
Back to contents ↑
Supplement
1. Scientists’ opinions about this work
V.V. Bushuev,
Doctor of Science, Director of the Institute of Energy Strategy: I share Yuri Ivanov’s hypothesis that driving force is
caused
by frequency (or phase) difference between two independent, but linked by
waves, oscillators each of which reflects the essence of elementary material
object. Whether these oscillations of magnetic or some
other nature, in my view, it’s not important.
I.P. Kopylov, Doctor of Science, Faculty Head of Moscow Energy College: What’s
new in it is that gravitational attraction, and any motion in general, is
explained by the super small gradients of phase and frequency. The majority of
researchers overlooked this aspect of the question.
V.A. Ilyin, Doctor of Science: The author of rhythmodynamics succeeded in not
simply giving the empirical formulas of classical mechanics the actual physical
meaning, but in much more: in eliminating the dividing line between classical
and quantum mechanics. This happened at the time when classic speed and
acceleration were expressed in formulas through phase displacement and
frequency gradient respectively.
A.I. Burenin, Professor: For the first time not just gravitation phenomenon, but
of all natural phenomena of force have received coherent scientific explanation
which doesn’t depend on questionable views on world organization. Undoubtedly,
such approach is a discovery which by right claims the status of the law of
nature.
Back to contents ↑
2. Science: privatization of truth
Natural
phenomena do not require recognition: they simply are, like it or not. But
their interpretation is prone to subjectivity, the interpreter’s talent as well
as the condition of society which is the main customer of scientific
interpretations. A society of feudal level of development requires appropriate
interpretations, like existence of a philosopher’s stone with the help of which
one can obtain lots of gold from lead. Capitalist society with more pragmatic
collective mind requires a more businesslike concrete approach. So each time
‘scientists’ emerge to fulfill social order.
The men of
reason know that although fundamental science may serve temporary interests of
applied research it, nonetheless, has no communist, capitalist or national
tinge. Science either is, or isn’t. But how can one tell science from fiction?
Modern views on
objectivity of scientific knowledge are rather varying. For example, relativity
theory which has mystified the minds of several generations of researchers. It
is still not clear if time slows in the moving system, or it slows down in motionless
one which moves relative to the moving system? The modern wise men are
interested in such scientific mysticism: one can make a good profit answering
allegedly vital questions posing mankind. Lots of these wise men are well aware
that they are actually ordinary conmen. But such confession would mean their
expulsion from ‘science’, the only source of these ‘wise men’s subsistence. So
you can imagine what might happen should someone come to expose their
‘tricks’. In short, the old saying that “the road to knowledge is measured by
inquisition fires” still holds true.
Financing is the
main factor in science. But what research receives money under capitalism? Only
the work which brings quick returns and easy political dividends. Such are
capitalist rules. All know this is wrong, and cannot go on forever.
So what’s to be
done? Apply for foreign grants? Or plunge into business themselves so as to
finance one’s own research?
One could also
ask for private business donations, but there are few businessmen in Russia who want to know what our world really is.
* * *
Competition
between scientific schools is really mind as well as science disturbing
process, particularly if one speaks about formation of its fundamental
elements. The modern world of science is affected not so much by the
competition of ideas as by the fight for financing, a reflection of a general
social scramble for better life. The winners are always those with stronger
administrative power and media backing. Under such conditions any competition
in the sphere of ideas is nipped in the bud. Sometime they simply steal those
ideas. The fundamental science of the 3rd millennia is driven by the
law of the jungle where might is right! Obviously for this very reason, to
preserve the status quo, a commission to fight pseudo science was created in
1998 under the auspices of the Russian Academy of Science.
But will this
commission really protect science, or simply defend the cushy seats of bureaucrats
in science?
Competition
between various technologies and their creators is quite justifiable: these technologies
are to improve peoples’ lives and accelerate the pace of progress. But how can
one justify competition between those lines of research which are supposed to
reveal the fundamental essence of our world and answer such seemingly simple
questions as how the world was created, what proto-elements it consists of,
what hidden processes form the basic properties of material bodies, like mass
(inertia), motion (ability to move in space), force (ability to interact). All
these properties are still thought inherent!
One should
stress the fact that supporters and followers of quantum mechanics and
relativity theory have been trying for over 50 years to convince the pubic that
these theories and none other have reached the ultimate truth.
One should
understand that people of Newton, Maxwell, Lorentz, Puancare, Einstein, De
Broile standing are not born every year; they are too few, while their
followers are numerous. And these followers, especially those with bureaucratic
background, are eager to reap the fruits of the glory which belongs not them,
but the founding fathers. Trying to conceal their mental inaptitude they are
doing their best to block the progress of new ideas by organizing struggle with
the so-called pseudo-science or by falsifying the results of scientific research
which they’d brought in and backed.
The current
commercialization of fundamental science, in effect privatization of the right
to announce truth is even a more bizarre phenomenon which might be viewed as
the ‘enemy action of aliens’ seeking to fool the naïve mankind.
So what are
independent researchers doing in such situation being excluded from privatized
science? Surprisingly enough, instead of trying to unite in their common effort
to survive as a species they are dying out, one by one.
Over the past
two decades the majority of those who chose to stay in Russia, either have taken leave of their senses, or switched to business, or passed away. Those who
are still alive and struggling is an interesting bunch to observe, especially
their pathetic attempts to find a niche in the privatized science, hoping that
bureaucrats would notice their efforts and give them some scraps from their
dinner-table.
There is some
logic in the current tragedy of the Russian science demise, so should one after
all try to do something to stop it?
Back to contents ↑
3. The number of space dimensions
Human
consciousness can grasp five (!) orthogonal dimensions in space + time as
motion characteristic. Overall, six!
Orthogonality of properties – mutual
statistical independence between parameters. The language of geometric models
expresses each parameter as a vector, a correlation is a cosine of the angle
formed by vectors. In this context independence is zero value of cosine reached
with the angles of 90 and 270 decrees (mutual perpendicularity).
Perpendicularity
is a sign of orthogonality, i.e. all listed coordinates must be perpendicular
to each other. In clear geometrical form only three coordinates: x, y
and z meet this condition. But there’s another sign of orthogonality.
If object moves
precisely along one axis of coordinates, and the object’s coordinates in other
axises do not change, this axis of coordinates is orthogonal.
Only in such
case the axis of coordinates may be recognized as orthogonal and used for dimensional
measurements. This condition is met by coordinate axises
 , where
, where
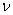 is frequency axis of
coordinates,
is frequency axis of
coordinates, 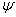 is a coordinate axis
toward zero-amplitude states.
is a coordinate axis
toward zero-amplitude states.
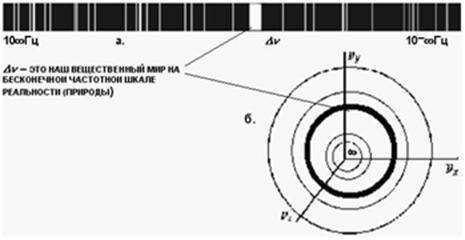
Fig.119 Referring to the question of frequency band:
on infinite frequency scale our world seems imperceptible spectral line.
If object
changes its frequency state, it or its parts are moving only along frequency
axis of coordinates. The object’s coordinates in other axises remain
unchanged. Each object has its own frequency interval, frequency form and
frequency depth. Space too has frequency depth ranging from infinity to zero (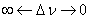 ). Our world and every object in it is limited by frequency interval
). Our world and every object in it is limited by frequency interval in frequency axis. Different frequency intervals coexist in a
single space. It’s similar to different radio stations’ frequency bands:
information broadcast by radio stations coexists in a single wave (ether) space
and doesn’t interfere with each other.
in frequency axis. Different frequency intervals coexist in a
single space. It’s similar to different radio stations’ frequency bands:
information broadcast by radio stations coexists in a single wave (ether) space
and doesn’t interfere with each other.
Fig.120 The object’s shift in frequency or to zero
amplitude may lead to interesting effects of materialization and
dematerialization, i.e. the object is present, but its material part is present
either in other frequency band, or in other amplitude (zero-amplitude for us)
reality.
Coordinate
toward zero-amplitude states is slightly more difficult for comprehension. If
we superimpose waves in opposite phases and eliminate amplitude, the wave
energy is transformed, for us, into zero-amplitude state, i.e. it exists but
for observer it is situated in a different sphere of being, in other amplitude
dimension. It’s this coordinate axis we are talking about.

Fig.121 There are no miracles, there is lack of
knowledge and ignorance, which is unwillingness to learn!
Perhaps, there
is depth of other amplitude realities, i.e. each zero-amplitude state in its
reality is perceived as amplitude one, and can be transformed into a more
zero-amplitude state.
Back to contents ↑
4. Space expansion and the Alice’s effect
“How do you know I’m mad?” said Alice.
“You must be,” said the Cat, “or you wouldn’t have
come here”.
Alice’s Adventures in Wonderland by Lewis Carroll.
Let’s expound
the RD hypothesis, according to which ‘space expansion effect’ and corresponding
to it the ‘red shift’ of fringes are supposed to be explained not by space
expansion but by synchronous shift along frequency coordinate of all visible
objects (stars, galaxies) present in space.
According to the
RD scenario, the Universe is not expanding, it’s the objects present in it
which are synchronously shifting its frequency toward its rise. This leads to
synchronous change of parameters of all instruments of measurement. For
example, the standard of length after higher frequency shift becomes physically
shorter, i.e. the observer with all his measuring attributes shrinks in size
and therefore perceives the Universe increasing in size, i.e. expanding (Alice’s effect).
According to the
hypothesis, in metrical space all objects remain in their place, whereas in
frequency space they are ‘flying’, i.e. their material essence is moving with
certain speed along frequency coordinate (the objects are ‘falling’ in
high-frequency infinity). Should such frequency shift proceed at a higher
speed, a situation might emerge in which now visible distant objects could
become invisible, being shifted relative to the observer on the earth into radio
frequencies band, while expansion would be perceived by the observer as
proceeding with great speed.
The same
dependency becomes the feature of Universe expansion at the expense of objects’
shift in frequency space: the farther the object from the observer, the
stronger is the fringes’ shift toward the red due to the time delay of the
incoming signals (photons). It’s easy to mistake such shift for Doppler’s
effect and suggest a hypothesis of a big bang and running away galaxies. Some
tend to regard as more logical the ideas of expansion of the space itself between
the galaxies, also leading to the red shift.


Fig.122 Having drunk the magic potion Alice shrunk, and, therefore, the room in her perception became more spacious…
To this RD
hypothesis I’d like to add information about one important consequence. Within
this hypothesis there’s no need talking about photon’s ageing as photon remains
exactly the same it was emitted at some time in the past. The answer is that
during its (photon’s) ignifycant time in transit the system of the observer on
earth has shifted its position on frequency axis of coordinates, and therefore
the observer’s standards of measurement have changed too, by increasing their
frequency. In such case we should talk not about Doppler’s effect which is
always linked to speed, but about the shift of the standards of measurement
toward the ultraviolet part of the spectrum. In effect, the observer is dealing
with an illusion strongly resembling the Doppler’s effect. This is a different
kind of effect and it requires some other name so as to tell them apart.
So, if all
distant objects change synchronously their position only on the frequency axis
of coordinates, i.e. shifting frequency toward its increase, a situation
emerges in which the observer receives information from other objects with
delay whereas its assessment is implemented by the frequency standards which
have changed in the meantime. As a result, the observer either has the illusion
of a big bang and running away galaxies, or ageing photons. But one can examine
the situation in a reverse order: i.e. all visible objects in the Universe used
to form a single body. This body, following the shift in high-frequency direction,
split into parts, which, in their turn, became divided into galaxies, stars,
and planets…
The term ‘Alice’s effect’ emerged from the
context of the book Alice’s Adventures in Wonderland by Lewis Carroll in
which his heroine Alice having taken a magic drink finds herself shrinking in
size, and appropriately, in her perception the space around her grows, expands.
* * *
Back to contents ↑
5. Comparison of the rhythmodynamics and
classical
mechanics formulas
|
Parameters |
CM formulas
|
RD formulas
|
|
Speed
|
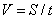 |
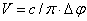 |
|
Acceleration
|
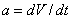 |
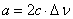 |
|
Quantum of mass
|
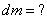 |
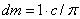 |
|
Impulse
|
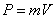 |
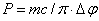 |
|
Force
|
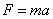 |
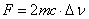 |
|
Centrifugal force
|
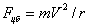 |
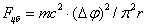
|
|
Kinetic energy
|
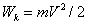 |
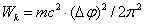
|
|
Standing wave length
|
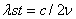 |
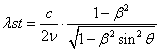 |
|
Energy flow speed
|
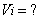 |
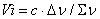
|
Back to contents ↑
6. Action without counteraction
One can find support only in something
which can resist!
Classical mechanics is based on Galileo-Newton’s laws which, though
considered unbroken, fail to explain the main thing, the inner processes which
form the essence of phenomena these laws describe. There is another line of
science, quantum mechanics which seeks to explicate the essence of the inner
processes. These two lines have a missing logical link which is supposed to
bring them together and without which they exist separately despite the
continuous talk about the necessity of unification of quantum and classical
approaches.
I think such unification has practically been achieved because with
rhythmodynamics the formulas of classical mechanics have acquired phase,
frequency, the speed of light and Planck’s constant – the attributes without
which quantum mechanics cannot exist. The phase-frequency means of presenting
the old mechanics’ formulas fills with real physical sense both the formulas
themselves as well as the notions which until now remained unclear: the cause
of motion, force, speed, inertia, gravitation. In this aspect, the developing
rhythmodynamics is rapidly bridging the rift between the two main lines in
physics, bringing them closer together. But let’s change the vector because
the present article examines cases when Newton’s third law is not implemented directly.
Newton formulated the 3rd law of motion
the following way:
‘To every action there is always opposed an equal reaction: or the
mutual actions of two bodies upon each other are always equal, and directed to
contrary parts’.
Some of Newton’s followers interpret the third law literally: in
nature there is no one-sided action of one body on the other, but there is
always interaction! Does this imply there are no situations of action without
opposite reaction?
It must be emphasized that Newton’s 3rd law applies only
to the ideal closed systems where action and opposite reaction are not
dissipated, but fully 100% realized. For example, when you affect an iron body
with a magnet you find that the iron body too starts affecting the magnet, i.e.
it starts attracting it with the same force. It happens because in the course
of magnetic field action the iron object becomes itself a source of magnetic
field (fig.123). Here the magnetic field, as a special state of surrounding
environment, plays the role of a medium, i.e. between the body and magnet it
exists on its own.
Fig.123 Interaction of a magnet and iron body M. Here
action equals opposite reaction, i.e. Newton’s third law of motion is realized.
The magnetic
field created by electric current is thought to propagate with the speed of
light. If the current’s impulse is short, the magnetic field having separated
from conductor keeps on traveling no matter if the conductor has at the moment
electric current nor not.
If the distance
to the body is big the magnetic field for the time being is situated between
the source and the object and exerts no influence on the body. In this sense
the portion of magnetic field en route from the source to the body can be
regarded as independent moving ‘entity’, i.e. the space by itself transfers its
changed state (magnetic) from one place to the other. During this period
magnetic properties in their portion form can exert influence neither on the
source from which this portion has already separated, nor on the object which
it hasn’t reached yet.
Having reached
the object magnetic field changes the object’s state. If this action results in
the object’s turning into a source of magnetic field, part of the field is re-emitted
toward the initial source, i.e. for the time being the object itself turns into
a source and thereby can influence the initial source. In this situation the
‘action-reaction’ principle works because a back link exists.
If the back link
does not emerge in the course of one body action on the other, the law of action-reaction
doesn’t work in the system. Let’s show this on mechanical experiments in which
the back link between the objects is absent.
Suppose, we had
a device (fig 124) expelling two air jets in opposite directions in such a way
that jet forces are fully neutralizing each
other, while the downward expelled jet is neutralizing gravitational force as
well. In such case our device would stay suspended in air, i.e. it would have
zero weight.

Fig.124. The heavy ball suspended in the jet of air
exerts no pressure on the source. This happens due to absent back relation
between the ball and the source. If you had such device, you could hold the
ball without feeling the ball’s weight. The reason: the ball is suspended at
the expense of kinetic energy it receives from the jet, and it cannot affect
the source through the jet. Even if you were applying downward pressure on the
ball, i.e. significantly changed its position in the jet, even in this case the
device wouldn’t feel any pressure. The picture shows the device connected with
a hose to a powerful compressor.
For us the
absence of the device’s weight is apparent, therefore we can freely move the
device on condition of its initial (vertical) orientation in space.
Let’s change the
situation and put a ball (a body of stable form for such kind of suspension)
weighing 10 kg. in the upward air jet so that the jet could keep the ball
suspended at a certain distance, say 5 centimeters. Would the device with zero weight react to a new situation, i.e. emergence of the
ball? Would the device’s zero weight increase by the weight of the ball suspended
in the air jet (0 + 10)?
No, it wouldn’t:
 [kg]
[kg]
There’s no
mistake about it. It’s only an illusion that the ball is propped by the jet and
through it exerts pressure on the source. In effect, the ball is isolated from
the system and suspended at the expense of kinetic energy passed to it by the
jet. This is easy to check in home conditions if you stage your experiment in
the bath-room:
Remove the spray
from the shower hose, direct the jet upwards and, holding the hose with one
hand, to measure weight try with the other hand to exert pressure through the
jet on the hose. You might be surprised to find that the hand suspended by the
jet or any other body suspended in it exerts no pressure on the source.
At first glance
the situation seems paradoxical, but it’s this situation which illustrates
possibility of application of force without incurring counterforce. Thereby
action can be one-sided, i.e. it may not trigger opposite reaction in the form
of pressure on the source of action.
In the same
unusual way, provided the device had sufficient capacity, one can suspend the
ball of a greater weight, say 100 kg., and freely move it with the device’s
help at the same time experiencing no additional (100 kg.) weight in the jet. This is possible only if the back relation between the body and the
source is absent, i.e. the body suspended in the jet has no possibility of
influencing the source of power. Thus we are able to not just hold and transfer
the heavy ball without any additional effort, but lift it to any height too. In
effect, we are dealing with a new gravidynamics paradox.
Fig.125 One of the devices to demonstrate action
without reaction is made in the form of a beam balance (published first time).
The balls of steel of different weight placed in jets exert no influence on the
beam balance.
I wonder how in
such case one should solve the problem of this type: Suppose, a body weighing 10 kg. were suspended in a powerful air jet (fig.124) in such a way that it doesn’t affect the speed
and direction of the jet expulsion from the source’s nozzle. How much energy
should one spend to raise this body to the height of 20 meters? (What’s implied is that a person should take the device which keeps the ball in suspended
state and climbing up the ladder should lift the body suspended in the jet to
the height of 20 meters).
If this problem
is solved correctly (the problem stipulates that the person with the device and
the ball climbs the ladder himself), the solution is to show that the person
will spend energy only to lift the device which creates the jet. The person
moving upwards with the device won’t even notice the presence of the 10 kilo
body in the jet (the essence of this paradox).
The situation
only seems paradoxical, but it has its explanation.
The action
without reaction effect can be organized in the ultrasound field of a powerful
source. Such experiment was conducted in one of the secret laboratories. Water
was used as acoustic medium. Heavy objects easily surfaced from the bottom of
the pool, i.e. behaved as if they had no weight.
Similar
phenomena, but of a different physical level, occur occasionally in nature.
Incidentally, ‘phenomenon’ is called this way because it happens suddenly and
cannot be studied in laboratory conditions.
“A globular
lightening of a football size flew over Galtsovka village in Altai region at
the height of twenty-thirty meters. The first obstacle in its progress, a shed
with concrete poles was crushed and brought down. Passing over a house with slate
roof-top the globular lightening tore off the slate from the roof and lifting
it in the air dragged it along, scattering it across the village.
Passing over a
tractor station, the lightening crushed one of the steel covered with canvass
carcasses, approaching the other carcass the lightening first dragged it on the
ground, then when it overtook the carcass the lightening lifted it into the air
and carried for 300 meters. The carcass itself remained intact. Its weight was
no less than 100 kg”.
After which the
author [20] examines situation trying to explain it by the laws of physics we
know:
“The fields of
the flying globular lightening carried the carcass weighing over 100 kg. And for some reason it flew in a strictly rectilinear fashion, totally unaware that some
steel carcass got stuck to it. If globular lightening is really thought to have
air’s density and weighs nothing, why did the carcass weighing no less than 100 kg. fail to alter to the slightest degree the trajectory of its flight?”
It’s worth note
that in some cases the field of the globular lightening repelled objects, and
in others it attracted them. This can have only one explanation: in each
specific case the field of the lightening had a specific impact on internal
characteristics of the objects after which the objects reacted by this or that
movement to their new state. Absence of the back relation (this happens
differently between the magnet and iron object) allows the globular lightening
to ignore the developments in its field. Had the objects themselves become the
sources of similar field, i.e. re-emitted it, they would have altered the
lightening’s trajectory. In this particular case we most likely have a
situation when action was not met with reaction.
Conclusions:
Within the
framework of familiar laws of physics an isolated task of direct action without
reverse relation has been formulated and solved. Solution of this task allows
us to reach a deeper understanding of how weight characteristics of material
bodies in open systems can be manipulated. As in the case with the jet example
(which is only an illustration of more fundamental processes) we can ‘deceive’
nature provided we have a really deep understanding of the inner processes
which form the phenomena under study.
In the case with
the ultra-sound example we can see that there are field flows which can influence
bodies without incurring the effect of reverse relation. Conditions and
criteria for the bodies and means of influencing them have been defined in
which direct realization of Newton’s third law of motion is absent (not to be
published in this article).
What matters is
not how much energy was spent to hold or transfer the body, but what parameters
and how this energy managed to change in the body itself. Sophisticated
changes in the body would trigger the body’s equally sophisticated reaction.
One could call
‘pressure’ the type of influence cited above, but examining the proceedings at
atomic and deeper level, i.e. from rhythmodynamics positions, we discover something
different, of phase-frequency nature, which opens our eyes. This different
gives us a clue as to what technologies of the near future we might have, and
what flying machines we are to build soon. But not all are capable of seeing
such fantastic perspectives.
Comments
In gravitational
field, we have a balanced open system in which the emergence of a new body at
first glance is supposed to trigger reaction of this system in the form of
weight increase. But this is not so.
Such task is
solved in two independent stages: 1) examination of interrelation of the source
of the flow with the flow itself (jet effect which is compensated by reverse
flow in the device); 2) examination of interrelation between the flow separated
from the source and the body (impulse in a unit of time on a unit of area). One
cannot examine interrelation between the source and the body because the flow
has no rigidity. For example, the flow of water can be regarded as small drops
with no tie between them. An interim flow split into drops cannot influence the
source in any way, that’s why action-reaction principle applies in each
particular stage, but not in overall case. If so, Newton’s third law of motion
must be expanded:
In an open
system with an intermediary between the bodies and 100% reverse relation the
indirect actions of the two bodies on each other are equal and aimed in
opposite directions; in the absence of reverse relation the indirect action of
one body on the other triggers no opposite reaction, i.e. reaction doesn’t
equal action.
Although this
definition requires further clarification it signals entirely different
approach!
* * *
Back to contents ↑
7. Rhythmodynamics and vibrational mechanics
Let’s examine an
example from vibrational mechanics [1]: self-synchronization of unbalanced
rotors (rotors the axis of which doesn’t pass through the center of mass).
“…two or more
rotors unlinked with each other kinematically and electrically mounted on a
common movable support and powered by independent asynchronous motors happen
to rotate synchronously – with equal or divisible average angular velocity and
with definite mutual phases. Rotors’ synchronicity emerges even despite
difference between their partial angular velocities, i.e. those velocities with
which they rotate when mounted on a fixed support. (fig.126). The inclination
to synchronous rotation in many cases is so strong that even switching off of
one or several motors doesn’t break synchronicity: the powerless rotors can
rotate endlessly. The energy required to maintain their rotation is supplied by
the working motors thanks to the vibrating support on which the rotors are
mounted. This vibration can be hardly noticeable so observer V might imagine
that these rotors are linked somehow.”
Fig.126
Self-synchronization of mechanical
vibration exciters. Two or more unbalanced rotors powered by asynchronous
motors on solid support have different rotation velocities
w1
and w2 (à). If mounted on a common movable support
they rotate with equal general velocity w (b). Synchronicity may be preserved
even if one of the motors is switched off (w1=0 or
w2=0). Observer V may have an illusion that
rotors are linked by a spring (c).
Let’s stage an
simulated experiment, and first change conditions: Suppose, the system of unbalanced
rotors (fig.127) mounted on a fixed platform is situated in outer space, i.e.
no external forces are applied to it. The system of rotors will create
longitudinal oscillations (compression-expansion) in the platform’s body the
material of which determines the speed of oscillations’ propagation. Suppose,
between the two rotors
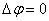 , and a standing wave
emerged in the platform’s body, in the nodes of which rotors are placed. In
this case the sum of internal forces in the system equals zero.
, and a standing wave
emerged in the platform’s body, in the nodes of which rotors are placed. In
this case the sum of internal forces in the system equals zero.
Fig.127 A ‘mechanical’ standing wave has emerged in
the platform’s body. Phase displacement leads to the break of synchronicity
and shift of nodes and anti-nodes (the standing wave energy is shifted to the
left).
Suppose, a phase
displacement  between the couples
of rotors has been implemented by internal means, the displacement which is
firmly fixed and thereby prevents self-synchronization. How will this system
behave itself in space? Will it develop a tendency to move in the form of
internal force? The more so that the potential holes (nodes, the areas of
energy comfort) are shifted relative to the sources, and one of them is even
beyond the platform’s limits. How can such discordant system restore
synchronicity? By its motion in wave medium?
between the couples
of rotors has been implemented by internal means, the displacement which is
firmly fixed and thereby prevents self-synchronization. How will this system
behave itself in space? Will it develop a tendency to move in the form of
internal force? The more so that the potential holes (nodes, the areas of
energy comfort) are shifted relative to the sources, and one of them is even
beyond the platform’s limits. How can such discordant system restore
synchronicity? By its motion in wave medium?
If such motion
is to take place in the experiment its speed is supposed to be insignificant because
the link with wave medium via low-frequency mechanical vibrations is quite
small. But one cannot give any definite answer until such experiment is staged.
Back to contents ↑
8. Phase-frequency tension and gravitational metrics
Is it possible
to describe gravitational cause through the notion of ‘space curvature’? It is,
at the same time one should understand that we are dealing with a mathematical
expression which may have nothing to do with reality. The other matter is when
we are talking about distribution in space of certain, say, frequency, characteristics
which create in the course of bodies’ motion illusion of curvature. In such
case the cause of gravitation could be more easily and gracefully described
within the framework of classic logic without any use of ideas of the general
theory of relativity.
For example, in
rhythmodynamics all types of motion and interactions are expressed through
phase displacement and frequency difference. The description is based on two
simple formulas:
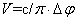 è
è
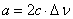 . In such
case force too (
. In such
case force too (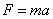 ) acquires
phase-frequency expression:
) acquires
phase-frequency expression:
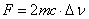 .
.
This also
applies to gravitational interrelation in which body M, say the Earth, creates
such conditions in space around it in which, once a test body get there, its
frequency parameters become asynchronized. The reason is gravitational red
shift and experiments based on Mossbauer effect. As a result of such
asynchronicity the so-called ‘spider-effect’ emerges, i.e. deformation and
sliding of its own internal interference field toward the Earth. In other
words, inside the test body the area of energy balance (comfort) moves in some
direction and drags atoms in its wake. Outwardly, it looks like a free fall.
Frequency
discordance is purely the system’s internal response to the emission created by
the Earth’s presence and in which this material system finds itself. That was
the reason why the notion of frequency gradient of space, or frequency tension,
was introduced in describing the state of space:
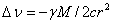 [Hz]
[Hz]
In this sense
Dn is a frequency gradient
of space, frequency tension which depends on mass M and distance r.
Now
the tendency to gravitate can be expressed in Hz, the fact to which one
has to get accustomed. (In case of the Earth on its surface
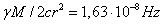 )
)
Frequency
gradient (tension) guarantees bodies a strictly definite in magnitude and
direction discordance of internal phases and frequencies, and, correspondingly,
concrete measure of disbalance of their inner comfort. Emergence of frequency
discomfort in bodies leads to their auto-reaction, i.e. to their
self-propulsion toward increased frequency tension. In this sense the
once-sided frequency discordance throughout the body is the nearest cause of
the masses proclivity to gravitate toward each other.
Derivation of
the formula:
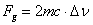 –
rhythmodynamics expression
–
rhythmodynamics expression
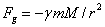 – classic
expression
– classic
expression
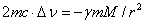 , therefore
, therefore
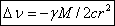
*If at the level
of the Earth’s surface
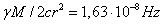 , at the level of the
Moon’s orbit the frequency potential (frequency tension) will be equal
, at the level of the
Moon’s orbit the frequency potential (frequency tension) will be equal
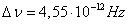 . This corresponds to the acceleration of the free fall
. This corresponds to the acceleration of the free fall
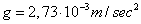 (here and further on acceleration is described by formula
(here and further on acceleration is described by formula
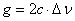 ).
).
Let’s compile a
comparative table of frequency tensions and accelerations which take place on
the surface of the bodies of our solar system.
|
System’s
object |
acceleration
[m/señ2]
|
tension
Dn [Hz] |
|
Earth |
9,8
|
1,63•10–8
|
|
Moon |
1,66
|
2,77•10–9
|
|
Sun |
274,4
|
4,57•10–7
|
|
Mercury |
3,92
|
6,53•10–9
|
|
Venus |
8,82
|
1,47•10–8
|
|
Mars |
3,92
|
6,53•10–9
|
|
Jupiter |
26,46
|
4,41•10–8
|
|
Saturn |
11,76
|
1,96•10–8
|
Frequency
tension at the level of orbits of the planets of solar system
|
System’s
object |
Radius
[km] |
Tension
Dn [Hz] |
|
Sun (on its
surface) |
695•103
|
4,57•10–7
|
|
Mercury |
58•106
|
6,56•10–11
|
|
Venus |
108•106
|
1,89•10–11
|
|
Earth |
149•106
|
9,94•10–12
|
|
Mars |
228•106
|
4,25•10–12
|
|
Jupiter |
778•106
|
3,65•10–13
|
|
Saturn
|
1430•106
|
1,07•10–13
|
|
Uranus |
2712•106
|
3,00•10–14
|
|
Neptune |
4485•106
|
1,10•10–14
|
|
Pluto |
5721•106
|
6,74•10–15
|
*The tables and subsequent calculations cite estimated
data.
Such approach
allows us to draw a portrait of solar system’s frequency tension measured in
Hz, and compile a computer chart varying relative to the planets’ position.
One should
understand that the planets, too, bring in their alterations in the general
picture. For example, Jupiter at the moment of opposition creates tension in
the Earth’s area equal to
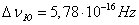 . This is
11.7 times less if compared with the Sun’s impact on Pluto, still it’s
significant enough to alter the Earth’s trajectory. Such magnitude can create
acceleration
. This is
11.7 times less if compared with the Sun’s impact on Pluto, still it’s
significant enough to alter the Earth’s trajectory. Such magnitude can create
acceleration 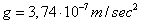 and alter the
Earth’s orbit by 1.3 km. in a single day, by 130 km. in ten days, and by 1166 km. in 30 days.
and alter the
Earth’s orbit by 1.3 km. in a single day, by 130 km. in ten days, and by 1166 km. in 30 days.
In a similar
situation the frequency tension on the part of Venus equals
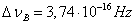 which corresponds to the Earth’s acceleration
which corresponds to the Earth’s acceleration
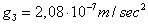 , and alteration of its orbit by 78 km. in ten days, and 700 km. in 30 days respectively. If the Earth is positioned between Venus and
Jupiter, the Earth’s deviation from its orbit will diminish significantly.
, and alteration of its orbit by 78 km. in ten days, and 700 km. in 30 days respectively. If the Earth is positioned between Venus and
Jupiter, the Earth’s deviation from its orbit will diminish significantly.
At present the
Earth’s frequency tension is also influenced by Saturn which is in opposition
jointly with Jupiter. Saturn’s contribution equals
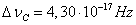 ,
which corresponds to the Earth’s acceleration
,
which corresponds to the Earth’s acceleration
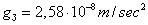 and
deviates the Earth from its orbit by 9.6 km. in ten days, by 87 km. in 30 days. As a result, the infinitesimal frequency gradients acting with surprising
steadiness can bend the planets’ trajectories. But such alteration has nothing
to do with the curvature of space.
and
deviates the Earth from its orbit by 9.6 km. in ten days, by 87 km. in 30 days. As a result, the infinitesimal frequency gradients acting with surprising
steadiness can bend the planets’ trajectories. But such alteration has nothing
to do with the curvature of space.
The system’s
response is, first of all, re-division of its internal energy relations which
under the impact of frequency tension leads to the emergence of vector
deformation. The system’s response is proportionate to the external impact of
body M on the given area of space and inversely proportionate to the
squared distance to M. Now we see that neutralization of gravitational
field is possible only through elimination of the frequency shift in the test
body, which is the task of antigravitational technology.
But what is the
cause of the bodies’ displacement of their own inner frequencies, what’s its
mechanism?
Rhythmodynamics
has pointed out a possibility of existence of a zero-amplitude field, ideally
made of waves without amplitudes (photons, gravitons). Amplitudelessness
provides for high penetration capability of these waves, their weak interrelation
with matter and other effects. But this is a separate serious topic for
research.
As for
gravitational waves which allegedly come to us every second from the depths of
the Universe, and on detection of which huge sums are wasted in order to
strengthen the entrenched misconceptions, well, to detect them a different
system of views is needed, and, consequently, a different methodology: not by
looking for space curvature, but by registering in concrete bodies concrete
changes of phase-frequency parameters. A different, though equally uphill,
task.
* * *
Back to contents ↑
9. Black Holes
Everyone in the
20th century knows about the Black Holes: “In keeping with the Newton’s laws and relativity theory, not even a quantum of light can escape a star
compressed to gravitational radius. The space where the black hole emerged is
curved and closes on itself” [14].

Fig.128. An artist’s view of the black hole. (Borrowed
from [1]).
When black holes
are discussed in scientific circles, the classic (diffuse) and ‘neoclassic’ (Burakan)
concepts of cosmogonic process are thought to be main ones. The first
originates from ideas and constructs of W. Herschel in late 18th
century; the second was proposed by V. Ambartsumyan in late 1940s.
Unlike
‘classics’ who regard Black Holes a natural step in evolution of matter, the
Burakan school postulate a hypothetical ‘pre-stellar matter’ as a relic
heritage of cosmological singularity. Pre-stellar matter is supposed to be
super-dense, being in a state beyond the influence of fundamental laws of
modern physics. In this respect, the Burakan school avoids physical detail
about the nature of hypothetical pre-stellar bodies which creates situation
when unknown is explained through a greater unknown.
Although the
black holes are regarded as exclusively theoretical(!) objects, representatives
of competing concepts seriously acknowledge possibility of their presence in
the Universe.
Academician
Vitaliy Ginzburg, supporter of ‘diffuse cosmogony’, indicates that “black holes
can exist within the framework of the general theory of relativity”.
Academician Ambartsumyan of Burakan school also thinks that “…existence of
black holes in the Universe is quite possible, being predicted by the general
theory of relativity”. Both schools regard the black hole a relativist object.
But there are other opinions too. For example, A. Logunov who created his own
version of relativity theory of gravitation thinks that black holes do not
exist [13]. Still…
What is most
interesting is the black holes’ matter which is concentrated in the central ‘no-single-point
singularity’ the size of ~10-33 cm
(Planck’s size). The fundamental laws of physics, including the general
relativity theory and quantum mechanics, are presumed not to work there. There
the black hole is regarded as an object which obeys the laws of physics unfamiliar
to us.
It’s the
material part of the black hole which causes the most heated debates. Still,
there are things in common, properties:
·
Super-powerful gravitational field;
·
Event horizon existence (Schwarzschild’s
surface);
·
Unobservability of matter crossing horizon in
the course of its collapse and continuing its movement toward central singularity.
These properties
are recognized by all schools of research, and it is thought therefore that
communication with the outside world for the collapsing object is impossible:
any particles (even photons) emitted from the black hole would return to the
black hole. Schwartzschild’s surface is a horizon beyond which an outside
observer can see nothing. Which means that the body which got into the black
hole becomes invisible after its crosses Schwartzschild’s surface. The general
theory of relativity suggests a unique interpretation here: a changed geometry
of space which became curved, closed on itself [1]. The presence of the
super-powerful gravitational field is also explained by space curvature.
To give a full
picture one should mention the ether concept which regards gravitation as a
consequence of the ether flow into matter [5,6]. If the speed of the flow
exceeds the speed of light, light is trapped inside.
So, there is a
problem of the black hole and there are several hypotheses which offer their explanations.
But is it possible, in keeping with scientific logic and operating only by the
known physical phenomena and effects, to give a different explanation of the
phenomenon’s properties? Let’s put questions:
·
What happens with the bodies between the distant
observer and black hole surface?
·
Why do bodies which have passed the
Schwarzschild’s surface become invisible?
·
Can one explain the super-powerful gravitation
without resorting to hypothesis of space curvature type?
·
Does the Schwartzschild’s surface block
electromagnetic waves?
Let’s give a
comprehensive explanation to the phenomenon, and outline the sequence of examination
of phenomena and effects by which we’ll be guided.
·
Gravitational red shift and
·
Wave concept of microstructure of matter;
·
Frequency pulling;
·
Deformation of interference field;
·
Gravitational drift;
·
Frequency horizon.
Gravitational
red shift
Among
gravitating masses the shift of frequency characteristics of matter takes
place. Gravitational red shift and Mossbauer effect are known there.
Experiments based on Mossbauer effect show that at atomic level a slow-down of
oscillatory processes takes place which depends on the distance to gravitating
body: the closer it is to the surface, the lesser is the frequency of
oscillations [1,7]. In conditions of the Earth such difference is practically
indistinguishable (the relative gradient 10-15 per 10 meters of height) but it can be registered by atomic clock. Such clock has a slower pace on the
surface than at some distance from it. Another corroboration of dependence of
the frequency state of material bodies on proximity to the gravitation source
is the red shift of fringes of chemical elements on the surface of stars. By
the size of the shift one can determine, for example, the mass of a distant
star: the greater is the shift, the more massive or dense it is.
Let’s examine
the mechanism of the shift of frequency characteristics.
Frequency
pulling in amplitudeless field
By the end of
19th century John W. Rayleigh observed
that two organ pipes with vents nearby start sounding in unison, if closely
tuned, i.e. mutual synchronization of vibrations takes place. Sometimes the
pipes make each other almost ‘silent’[4,8]. Here the competing source of
vibrations impose on each other their own frequencies. The degree of such
‘imposition’ (pulling) depends on correlation of capacities and distance
between them.
According to [1] matter has a wave origin and can be presented as a
package of standing waves with atoms in their nodes (fig.2). Every element of
matter (atom) is vibrating. If the minimal distance between atoms is determined
by a single anti-node (≈ 1–10Å), then one can make a judgment about the level of frequency of
these vibrations (≈1018Hz). In this sense matter is invisible for us because
the range of visual perception is much smaller (≈1014Hz). What
comes to rescue is the property of material bodies to reflect, or rather
re-emit the waves necessary for our visual perception. If matter is in excited
(plasma) state it starts emitting on its own the whole range of spectral lines
and thereby shows its wave nature.
From the
point of view of universality of world environment each atom of a chemical
element forms inside and around itself its own frequency interval (frequency
environment) within the ranger of which it is stable. When interacting with
other chemical elements, or atoms, a different frequency environment is formed
comfortable for the aggregation of these very elements and so on for any
aggregation of elements. Chemical elements or their combination can exist
comfortably only in frequency environments they formed and with any change in
the elements or their combination formation of corresponding environment
becomes condition of their stability. In other words, one cannot view matter
separate from its frequency environment. This is obvious considering that
various chemical elements consist of the same elementary particles, and what’s
important here is combination which can be stable only in certain frequency
interval. Acting on frequency interval leads to a reaction, or to the change of
chemical elements if such reaction proves impossible.
Taking into
account the above-said one can give a different interpretation to D.
Mendeleev’s table of chemical elements, which reflects only periodicity but
gives no explanation to it.
There are
interesting characteristics of frequency environment (field): density and
amplitude. The field’s density (thickness, saturation) depends on the number of
object’s oscillating elements and distance to it, i.e. diminishes with
distance. Amplitude is a different matter. If the number of oscillating
elements is big, any emitted traveling wave (quantum) can always be matched by
identical one but in opposite phase. A situation of amplitude annulment emerges
in which there are traveling waves but no resultant one. In this connection
calculations were made and 3-D modeling performed [4]. A theoretical
possibility of existence in nature of ‘non-emitting’ systems of oscillators and
wave amplitudeless fields was discovered.
The absence of
amplitude hinders possibility of registering wave characteristics of the field
and creates an illusion of absence of anything in space. In such cases the
field is referred to as a different kind of matter, but recognition of a
model-based way of a zero-amplitude propagation of wave disturbances makes it
possible to talk about the wave nature of the fields. Let’s dwell on
gravitational field which, according to the rhythmodynamics approach represents
a wave amplitudeless background of high frequency, ideally consisting of
amplitudeless (non-manifest) quantums, gravitons.
Absence of
amplitude makes it possible to talk about high penetration ability of
gravitational field: there’s nothing in it, so ‘it’ can penetrate anything. OK,
but isn’t there some way in which the bodies feel amplitudeless field? The
energy transfer from non-manifest amplitudeless state to manifest one is
presumed to take place in non-linear mediums. If non-linearity in the form of
material body can displace phases part of the energy is released. Apparently,
the release of this energy can be accounted for the emergence of frequency
gradient in the bodies. And may be for this very reason in gravitational field
the fringes of excited matter are shifted toward the red. Here’s analogy to
this: If you have a mechanical pendulum clock, the period of its fluctuations
in vacuum, air and water is different. The denser is the medium, the harder it
is for the pendulum to swing. The clock has a slower pace in water then in
vacuum, but faster then in liquid mercury. In this sense we can talk of
gravitational medium which imposes on the bodies which got into it its own
frequency rules of the game. In turn, the bodies too bring in changes – they
deform the general field.
Deformation
of interference field
One of the
consequences of the body’s presence in gravitational field is discordance of its
frequencies. The body is volumetric and discrete, i.e. consists of isolated
atoms which are positioned at various distances from the massive object. For
this reason the level of frequency pulling for each atom is different. Let’s
examine this issue in greater detail.
Let’s consider
the matter as a package of standing waves with atoms in its nodes (12).
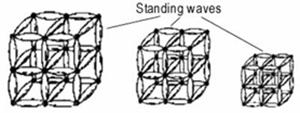
Fig.129 Atoms are the sources of waves. Standing waves
emerge between neighboring atoms and link the sources with each other. Wave
crystal lattices emerge (packages of standing waves) with atoms in their nodes.


a
b
Fig.130 a) Different distance between atoms and
gravitation source makes the level of their frequency pulling different too.
Frequency discordance takes place in the system; b) Frequency gradient leads to
deformation of interference field and its sliding off the object. Outwardly the
interference pattern resembles a spider, hence the name: spider effect,
gravitational spider. To this sort of deformation the system reacts by motion.
Atoms are
distanced differently from the surface. The space between the top and bottom
parts of the crystal (fig.130a) is measured in just a few angstrom which is
enough for a frequency gradient to emerge. Frequency difference triggers the
so-called ‘spider-effect’ (fig.130b) [4], i.e. deformation of the general field
of interference and deformation of internal relations. The latter implies a
directed shift of the nodes of the wave crystal lattice relative to atoms.
Atoms seek to stay in the nodes and therefore are forced to move constantly in
the nodes’ wake. The system starts moving.
Gravitational
drift and weight loss
The Black Hole
(here we refer to any source of gravitation) imposes a vector deformation on
the body which it seeks to avoid (get rid of deformation) by all means
available, one of which is motion in the wake of its own interference field.
Which results in drifting toward the black hole, viewed by us as a free fall.
If the cause of
the free fall can be described as frequency discordance, i.e. through internal
causes, there is no need to introduce the notion of space curvature. It would
be more logical to talk about distribution in linear space of potential
characteristics capable of creating energy discomfort in bodies.
As for
curvature, here one should turn to comparison of the standards of length positioned
in different places in space, the metrics of
those standards being tied entirely to the frequency state of matter.
Absence of
gravitation source guarantees equality of frequency states for the standards,
and consequently equality of their lengths (fig.131a). Appearance of a
gravitating body breaks frequency equality, the standards become unequal, i.e.
they cannot be used to construct linear figures which is associated with
curvature (fig131b). Whereas rhythmodynamics speaks of curvature illusion.
Fig.131
If gravitational
drift is caused by frequency discordance, the leveling of frequencies would
inevitably lead to end of the fall, i.e. to anti-gravitation [12]. The body
would lose weight (not mass) and hang up! But not ‘for free’, though.
Fig.132 Assuming levitation to be a potential human
ability, one might say that those rare cases known in history of its
manifestation, despite their exceptional nature, testify to a possibility of
weight loss at the expense of a changed inner state of human body.
Frequency
horizon
What happens if
relative to the observer the frequency characteristics of the object under
study were to move completely into infrared band? Such body is expected to
become invisible for the observer.
Something
similar might happen in the area near the black hole because in the course of
the body’s approach to it the body’s frequency characteristics are shifted in
the infrared band.
Suppose, the
body were falling from A to D (fig.133 b). For the observer A
the spectral lines of the body would be moving to the infrared band. He
watches the departing body first turning red, then disappearing. Visual
detection would cease the moment the package of spectral lines moved completely
in the infrared band. If another observer were to fall along with this body
he’d find himself in a symmetrical situation: the package of spectral lines
characterizing the state of A would move completely to the ultraviolet
band. It must be pointed out that none of the observers would notice any
frequency changes within his own system.

a b
Fig.133 To illustrate the event
two types of the clocks are to be used: real and imaginary ones (a). Picture
(b) shows gravitational red shift of spectral lines (frequencies) in systems B,
C and D relative to the scale of system
A.
One might say
that A and the falling observer ‘disappeared’ for each other, i.e. they
are separated by Schwartzschild’s surface. Though it would be much more logical
to explain this mutual ‘disappearance’ by significant difference in frequency
characteristics of the objects. In this sense Schwartzschild’s surface could be
viewed as frequency horizon: the disappeared observers actually stay
where they were before, and even can observe each other for some time with the
help of the infrared and ultraviolet vision devices.
Nor there is any
justification in banning the electromagnetic signals from leaving the black
hole, i.e. come out on surface. The other matter is what happens with the
sources of these signals, if the black hole matter were considered as such?
If everything is centered on the red shift and its dependence on
concentrated mass, then, with its appropriate accumulation, the frequency
characteristics of the falling matter which hasn’t reached the surface of the
black hole yet would be in radio frequency band. In this respect the body
falling on the black hole would behave like a radio source. But the frequency
state of the black hole increases (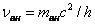 ).
).
Let’s summarize
the results of this simulated experiment:
·
For outside observer
A the objects
situated between the Schwartzschild’s sphere and the black hole body are
invisible because all their frequency characteristics are shifted toward the
infrared part of the spectrum.
·
For observer D situated near the black
hole surface the outside observer becomes invisible because all frequency characteristics
of the outside objects for him are shifted into ultraviolet part of the
spectrum.
·
With accumulation of its mass the black hole
turns into a super-highfrequency object while frequency parameters of the
falling matter will be shifting to the radio frequencies band.
Relativity of
frequency horizon
The black
hole matter forms appropriate medium inside and outside itself. Any material object
which enters or leaves it must change its frequencies appropriately.
We matched
frequency horizon with Schwartzschild’s sphere the radius of which is customarily
determined by the formula
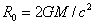 , i.e. the greater is
the mass, the greater is the sphere’s radius. In rhythmodynamics frequency
horizon is a relative notion, because it has a different physical meaning. So
the formula describing the horizon radius for a distant observer is different
too:
, i.e. the greater is
the mass, the greater is the sphere’s radius. In rhythmodynamics frequency
horizon is a relative notion, because it has a different physical meaning. So
the formula describing the horizon radius for a distant observer is different
too: 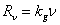 , where
, where
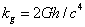 . Replacement of mass (M) in the
regular formula by its frequency state (
. Replacement of mass (M) in the
regular formula by its frequency state ( ) makes it possible to examine the phenomena and processes linked
with the black hole in frequency aspect. Now we can say: the higher is the
frequency of the black hole body, the bigger is the radius of its frequency
horizon. Unlike Schwartzschild’s sphere, frequency horizon is a relative
notion which depends on relation of frequency states of the ‘observer – object’
systems.
) makes it possible to examine the phenomena and processes linked
with the black hole in frequency aspect. Now we can say: the higher is the
frequency of the black hole body, the bigger is the radius of its frequency
horizon. Unlike Schwartzschild’s sphere, frequency horizon is a relative
notion which depends on relation of frequency states of the ‘observer – object’
systems.
If for observer
A
frequency horizon were defined by surface 1 (fig.133a), then object C
would be invisible for him. For observer B the frequency horizon is
different and defined by surface 2 that’s why object C is visible
for him. The reason is different relativity of frequency characteristics.
It’s interesting
that for observer C there may be two horizons: the inner one behind
which system D is hidden, and outer one beyond which system A
cannot be seen. System C and the observer happen to be isolated on both
sides but if objects with similar frequency characteristics are to emerge in
space, they will be visible for C.
Let’s examine a
hypothetical example with two black holes of equal frequencies, on the surface
of which there are observers D' and D. D' and D are in
equal frequency conditions therefore communication between them is possible.
But outside objects, say observer A, are invisible for them because of
the large difference of frequency characteristics.
Understandably,
A
cannot see D' and D either. Here it would
be proper to talk about frequency divided parts of a single space. For each
type of observers the world seems real only in their accessible frequency band.
Everything which stretches beyond this band seems to them beyond their
comprehension, i.e. beyond their frequency horizon.
In
this respect every world limited by frequency band would be perceived by the
other world as a kind of black hole!
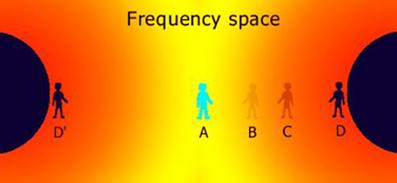
Fig.134 In the environs of massive bodies illusion of
frequency (pseudo-frequency) space emerges.
Objects’
materialization and dematerialization illusion
A material
object moving from D' to D (or vice versa) and passing by A would
behave quite weirdly: first, it would appear as if out of nothing, then,
departing, would disappear as if dissolved. The cause of this are changing
frequency characteristics of the moving object: when they fit into the range of
visual perception of A the object becomes visible. Further shift of
frequency characteristics leads to the object’s visual disappearance. But, as
was said before, the object could be observed for some time in the infrared
band with the help of special vision devices.

Fig.135 Illustration of frequency horizon issue. The
angle of reflection does not allow observer on the surface to see objects under
water, nor can observer under water notice a falling diver before he hits the
surface. The transfer through real and at the same time conditional border
between air and water is accompanied not only by disappearance of the object in
one world and its appearance in the other but by intensive wave disturbances on
the dividing line. The observer under water might think that spontaneous birth
(materialization) of the object took place, while the observer on the surface
might imagine it disappeared (dematerialized). In this example the border
between different frequency mediums is evident because our sense organs cover
both frequency bands. Interesting situation might emerge when different
frequency worlds (mediums) are encapsulated in their volume one in the other.
If frequency barrier is sufficiently big, i.e. cannot be bridged by our sense
organs, the transfer from one frequency band to the other would be accompanied
by effects of disappearance in one world and appearance in the other, and wave
disturbances of the conditional division line. These effects are not only
possible to calculate without the use of additional dimensions, they are also
comprehensible within our three-dimensional logic.
The mechanism of
materialization and dematerialization was described in my work “Frequency
space” [3]. It was also suggested there to use frequency as a
coordinate (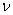 ).
).
Introduction
of a frequency coordinate seems a natural and logical step. With additional frequency
coordinate we have a chance of a deeper penetration into the root-cause of
things.
The motion along
frequency coordinate in free space differs from
similar motion in the field of the black hole.
On the outskirts
of the black hole the change of objects’ frequency characteristics is not
direct and is always linked with the transfer in metric coordinates. In this
sense the black hole creates conditions similar to frequency space.
Motion in
classical frequency space is different: the object, moving along frequency
axis, materializes and dematerializes without changing its position. Does it
mean that it’s physically absent in space? From rhythmodynamics positions, the object
is present but not visible.
We’ve come close
to the dividing line by crossing which we inevitably get into the other equally
real world. Such worlds can coexist with each other side by side being
separated by frequency horizon, and therefore visually, they regard each other
as ‘black holes’. They barely interrelate [11], that’s why such interrelation
is called sensual, informational [9] perceived at the level of intuition [10].
Conclusions:
·
Rhythmodynamics space has non-linear
distribution of frequency-amplitude characteristics (potentials, conditions)
which creates curvature illusion.
·
Frequency pulling is the cause of gravitational
red shift, slow down of the pace of atomic clocks, and frequency discordance.
·
Frequency discordance of the body leads to
directional (vector) deformation of interference field. The action of deformation
is countered by reaction of motion (free fall).
·
Massive body becomes invisible due to the shift
of its frequency characteristics toward ultraviolet part of the spectrum. In
such interpretation ‘collapse’ is viewed as a fast shift of the body’s
frequency characteristics.
·
The notion of ‘Schwartzschild sphere’ is
replaced by frequency horizon, once beyond it the object becomes invisible.
·
Electromagnetic waves freely pass through
Schwartzschild sphere in both directions.
Although until
now on the issue of black holes there were two antagonistic hypotheses: classical
(diffuse) one and Burakan one, with the publication of this paper a new point
of view has emerged, that of rhythmodynamics, which asserts that:
·
There are no curvature of space and black holes
in their usual sense but there is illusion: the
bodies become invisible due to the frequency
characteristics shift toward infrared or ultraviolet area.
·
Our universe is surrounded on both sides by
frequency horizon, and therefore is invisible for the outside worlds, i.e. being
a ‘black hole’ for them!
·
In the course of the black hole’s mass
accumulation its overall frequency increases until a moment comes when any further
frequency increase would lead to, first, weakening of gravitational properties
(because of weakening effect of frequency pulling) until their complete
annulment , then to the black hole transfer into other frequency band of space.
For residents of a different frequency dimension this process may look like a
birth of a new star, or an elementary particle.
Bibliography:
1.
Jay Orear. Physics. Translated
from English. Mir, 1981.
2.
Blekhman I.I. Vibrational
mechanics. Fizmatlit, 1994.
3.
Ivanov Yu.N. Frequency space. Novy
Tsentr, 1998.
4.
Ivanov Yu.N. Rhythmodynamics. Novy
Tsentr, 1997.
5.
Yarkovskiy I. O. Universal
gravitation as a consequence of formation of weight in matter of stellar
bodies. Kinematic hypothesis. Kushnerov publishers, 1912.
6.
Atsukovsky V.A. Hypotheses of
Etherdynamics. Petit publisher, 1997.
7.
Detlef Kamke, Klaus Kramer.
Physical foundations of measurement units. Translated from German. Mir, 1980.
8.
Strutt, John (Lord Rayleigh).
Theory of sound. Gostehizdat. 1944.
9.
Yuzvishin I.I. Informationology.
Radio i svyaz. 1996.
10.
Ivanova N.M., Ivanov Yu.N. Life by
intuition. Komplekt, 1994.
11.
Stavitskiy A.I., Nikitin A.N.
Speaking the language of nature. Intan, 1997.
12.
Ivanov Yu. N. Compression of
standing waves, rhythmodynamics and third state of quiescence. RIA, 1996.
13.
Logunov A.A. Relativist theory of
gravitation and Mach principle. Institute of high energy physics, vol.29,
edition 1, 1998.
Back to contents ↑
10. About Louis de Broglie’s law of phase harmony
By N. Nevesskiy
I’d like to tell
about the law of phase harmony formulated by Louis de Broglie in 1924.
This law is seldom mentioned in the papers on quantum theory, although it
actually kick started this theory, and despite the fact that de Broglie himself
thought this discovery of his was pivotal in his life.
Louis de Broglie
was born in 1892, into one of the most aristocratic families of France. He had the blue blood of French royal family, he was a duke, but despite his noble
standing he lead the life of ordinary people. Having graduated from a college
he entered Paris University and studied humanities: history, literature,
paleontology.
Later in his life
his knowledge of humanities benefited him greatly: he was excellent writer, and
his books on the most difficult issues of wave mechanics testify to this. He
was also an avid reader of the history of science works (he confessed he had
read more books on history than on physics), whereas his study of paleontology
had probably lead him to conclusion that all things were alive because even
seemingly lifeless stones kept the traces of life which had flourished millions
of years before…
When young, de
Broglie felt that his liking for science prevailed over humanities, he put
aside his recently acquired diploma and reentered the university to study for
science degree. After graduation he takes up research of the most crucial at
the time issue of quantum-wave dualism, an odd phenomenon but strikingly
manifest during experimental studies of light, as well as x-ray and
g-radiation.
His closest
teachers were Paul Langevin and his elder brother Maurice de Broglie. Maurice
who was 17 years Louis’ senior was at the time an acknowledged physicist who
took part in the first Solvay conference and who had a well-equipped laboratory
specializing in roentgen spectroscopy research. There the young Louis learned
the secrets of experimental science, grasped firmly the range of problems which
required solution and began tackling them. There his work as a theorist
started, and the results of it lay foundation for his doctorate thesis.
The law of
phase harmony became the central point of his
paper. The essence of de Broglie’s idea was brilliantly expressed by G. Lochak
[1], his closest pupil and aide.
On the one hand,
the idea seems simple, on the other, it’s a mystery how one could come to it.
The very train of thought was extraordinary. May be it was the result of some
sort of enlightenment, or it could be the result of a special way of De
Broglie’s thinking.
De Broglie, it
must be emphasized, had a very imaginative thinking. He stressed that for him
understanding implied very clear, as if real, vision [2]. There was no understanding
without image. The abstract mathematical method which physicists used was
strange to him.
De Broglie was
also a rabid supporter of relativism. Relativity theory had just emerged but
was already acknowledged, and De Broglie, too, was fascinated by its unusual
beauty. In a number of basic reasonings of relativity theory ‘observers with
clocks’ were used which was, in De Broglie’s opinion, a very apt revealing
image. ‘Observers’, according to the theory, were not theorists striving to
comprehend the developments in micro-world, but the residents of this world:
electrons, protons, etc.
Elementary
particles are those observers; which is important. All of them have their own
clocks and interrelate with each other through wave signals exchange. A very
powerful analogy which De Broglie, with his image thinking, accepted literally.
Elementary
particles, he reasoned, are complex systems (because only complex systems can
interrelate in such way). Each particle has its own inner periodic process,
which, on the one hand, serves as a measure of internal time (i.e. ‘tells
time’), on the other, provides for creation of those wave signals used in
communication.
For propagation
of those wave signals a medium was needed, and ether (in its classic sense) was
no good for this role as its use could lead to conflict with relativity theory.
Which De Broglie avoided by all means being a devout believer in relativity.
Later on he, nonetheless, introduced this medium in such a way as not to harm
relativity. But initially, in 1924, when he wrote his doctorate thesis, all his
attention was focused on ‘internal clocks’.
So, every
elementary particle had its own internal oscillatory process. It sets the scale
of time and functions as internal clock with the help of which the particle can
navigate in time. De Broglie doesn’t dwell on the process itself. What
interests him is process frequency, which he describes in his famous formula:
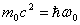 (1)
(1)
Both parts of this equation were known
before, but De Broglie was the first who brought them together. “That’s how it
should be, he wrote, due to the great law of Nature”.
This is the first formula in his thesis.
It was very beautiful, and could be the most beautiful, but for one thing. This
equation determines the frequency of inner process only in one’s own frame
of reference. After transfer to the other system it stops to work, being
not Lorentz-invariant. Indeed, in the case of a moving electron (he usually
referred to electron when speaking of elementary particle) mass increases like:
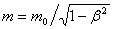 while the frequency of clock pace decreases like:
while the frequency of clock pace decreases like:
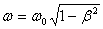 (here
(here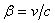 ). Thus, equation (1)
loses its validity.
). Thus, equation (1)
loses its validity.
De Broglie noticed this at once, and this
situation puzzled him greatly. He was bubbling with relativist ideas, which he
never doubted. He sought to defend the equation (1), but at the same time he
knew he wouldn’t succeed unless he made this equation relativist. De Broglie
solves this task, making a second, resolute and radical step by introducing the
notion of stationary wave.
Which meant the following: Suppose, he
said, the oscillatory process going on somewhere inside the particle at
frequency  is reflected (or
somehow permeates) outside so that in every point of space around the particle
an oscillation is initiated of exactly the same frequency. Or, in other words,
in every point of the Universe a clock emerges running in pace with the clock
of the elementary particle.
is reflected (or
somehow permeates) outside so that in every point of space around the particle
an oscillation is initiated of exactly the same frequency. Or, in other words,
in every point of the Universe a clock emerges running in pace with the clock
of the elementary particle.
Mathematically, this supposition could be
described by formula:
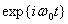 (2)
(2)
(In every point oscillatory process with
frequency 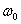 takes place. All
processes are in phase irrespective of coordinates).
takes place. All
processes are in phase irrespective of coordinates).
The same is true for its own system where
electron is motionless. If it moves time is transformed according to Lorentz:
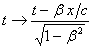 . As a result of which all clocks become asynchronized and equation
(2) turns into:
. As a result of which all clocks become asynchronized and equation
(2) turns into:
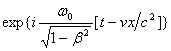 .
.
Which is the stationary wave.
It can be seen from definition. Its
frequency is 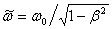 , i.e. it changes the
same way mass does. So equation (1) can be made relativist if its frequency
were referred not to the frequency of internal process, but to external one,
the frequency of Universe tuned to the rhythm of the particle. So ‘zeros’ of
(1) can be erased and one can write:
, i.e. it changes the
same way mass does. So equation (1) can be made relativist if its frequency
were referred not to the frequency of internal process, but to external one,
the frequency of Universe tuned to the rhythm of the particle. So ‘zeros’ of
(1) can be erased and one can write:
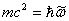
This formula is already relativist!
Stationary wave propagates with phase
frequency 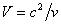 and its wave length
is
and its wave length
is 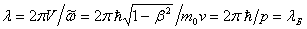 , where
, where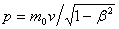 - frequency impulse.
- frequency impulse.
This is the De Broglie’s wave length.
So, De Broglie managed to make the
relation between energy and frequency Lorentz-invariant. But at what a price!
The general picture, compared with classic one, became much more complex. In
classics, when you examine a moving particle you deal with only one object,
this very particle. De Broglie has two objects to deal with: particle and
stationary wave linked to it. Both objects are independent, though related.
Incidentally, De Broglie has no
quantum-wave dualism at all, he has no notion of some ‘particle-wave’. This
physical centaur was born later, and it was introduced in physics not by De
Broglie but by other later interpreters. De Broglie regarded both the particle
and wave as independent entities, and he thought the wave to be physically real
wave.
Studying these two objects as independent
ones, he came to his famous law of phase correspondence or phase
harmony which says that “The moving electron is always in phase with its
stationary wave, or - the phase of stationary wave in the point of electron
position always coincides with the phase (inner clock) of the electron
itself”.
This assertion is easy to prove. The
phase which electron has in time t is
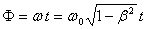 ,
while the phase of stationary wave in the point of electron’s position (with
,
while the phase of stationary wave in the point of electron’s position (with
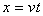 ) is:
) is:
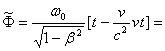
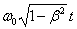 , i.e. the same
value.
, i.e. the same
value.
So,
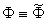 . But
what’s next? De Broglie thought the stationary wave linked with electron, being
physically real, can somehow influence the behavior of the electron itself,
once they are always in phase. Following this view, he studied hydrogen atom so
as to apply his assumptions in concrete problem solution and with their help
obtain the rules of orbits quantization. (Such rules had already been set by Niels
Bohr. They looked beautiful but were completely incomprehensible).
. But
what’s next? De Broglie thought the stationary wave linked with electron, being
physically real, can somehow influence the behavior of the electron itself,
once they are always in phase. Following this view, he studied hydrogen atom so
as to apply his assumptions in concrete problem solution and with their help
obtain the rules of orbits quantization. (Such rules had already been set by Niels
Bohr. They looked beautiful but were completely incomprehensible).
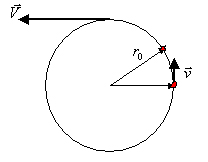
Fig.136
His reasoning was the following: Suppose,
says De Broglie, electron were moving in circular orbit with speed v.
The stationary wave linked with it moved in the same orbit and the same
direction, but with speed
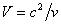 (i.e. much faster).
After some time
(i.e. much faster).
After some time 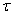 the stationary wave
catches up with the electron (fig.136). Time
the stationary wave
catches up with the electron (fig.136). Time
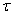 is
determined from relation
is
determined from relation
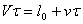 (where
(where
 – length of orbit), from which:
– length of orbit), from which:
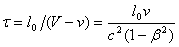 .
.
By this moment the electron accumulates
the phase:
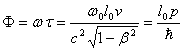 . And the same phase
is accumulated by the stationary wave.
. And the same phase
is accumulated by the stationary wave.
“It’s almost self-evident (in De
Broglie’s own words) that this phase should correspond to interger of
electron’s oscillations”, i.e.:
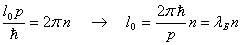
So, a whole number of De Broglie’s waves
(stationary wave lengths) must fit in the orbit. Hence is the outline of the
physical meaning of statement about a whole number of oscillations because only
in this case the stationary wave covering several times the circumference of
the orbit won’t suppress itself.
As
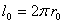 , where
, where
 is orbit’s radius, the latter equation can be transformed to:
is orbit’s radius, the latter equation can be transformed to:
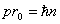
which is the second postulate of Bohr.
So, the notions introduced by De Broglie about internal process and stationary
wave proved quite effective if they allowed to obtain so easily the rule of
quantization of the impulse’s moment for Bohr’s orbits.
This was a certain feat appreciated by
everyone. De Broglie received unanimous acclaim from scientific elite; his
works were studied, and efforts were made to their advancement [3]. De
Broglie’s concept had definitely clarified something, but at the same time
raised lots of new questions. For example:
·
how (why) does stationary wave move in circles?
(Radial heterogeneity was apparently necessary for this which could have the
wave locked on itself due to internal reflection. This issue was studied by
Ervin Schrodinger);
·
what was exactly meant by “internal periodical
process?”
·
what’s ‘stationary wave’? Is some sort of medium
necessary for its propagation, if so, how is it to be introduced without
contradicting the special theory of relativity? How does it relate to electron:
is it born by (only) it, or is the whole Universe participating somehow in its
conception?
·
how does the stationary wave influence
electron’s behavior, and what is after all behind the law of phase harmony?
And so on and so forth, including the
question as to ‘what’ or ‘who’ is the electron? The idea of the electron’s free
will was quite seriously debated, in which N. Bohr himself took part.
In short, passions were running high, and
physics was rapidly developing. Schrodinger produced his famous equation. Bohr
suggested its probable interpretation. Calculus was rapidly developing, and
theory was acquiring quite definite outline.
De Broglie himself was working
incessantly. He was developing the so-called ‘double solution theory’ according
to which particles, remaining localized entities, were sort of inserted in the
wave in the form of singularities of a uniform solution. According to this
concept, the particles acquired sort of wave-like wings. The work progressed
slowly due to serious mathematical problems. One had to study non-linear
equations producing soliton-like solutions, which was not easy and required
time and strength.
Meanwhile, physics was pushing onward.
Though it moved in not quite the same way de Broglie chose, and with the help
of other, abstract mathematic means which were alien to de Broglie. “He was
witnessing the emergence of an entirely different approach to theoretical
physics. Which was based not on description of the laws of nature with the help
of space-time images, but on algebraic and geometric constructs in abstract,
usually complex and multi-dimensional spaces”[4].
Physics was replaced by math.
Surprisingly enough, this approach brought fruit. Theorists dived boldly into
mathematic abyss and brought up the treasure-troves in the form of elegant
formulas proved by experiment.
Such abstract method was alien to de
Broglie. He had an image thinking, which for him was a matter of principle. He
went his path, though he felt he was lagging behind, and could become a
straggler for good. In 1927, at the 4th Solvay conference he
nonetheless chose to fight and delivered a report about his double solution
theory, not yet completed at the time. The report went unnoticed. De Broglie
was not understood, nor supported, and he finds himself alone. The victory was
won by the indeterminist interpretation of quantum mechanics developed by the Copenhagen school (which is still generally accepted). After which the defeated de Broglie
leaves the scene.
Discouraged he returns to Paris where he teaches theoretical physics at the
Institute of Henri Poincaré. He suspends his
research being in a way convinced that the path he had chosen was wrong and the
right one was the main road chosen by the rest of the world physics. Amongst
others, he teaches quantum mechanics which he persists to call wave
mechanics sticking to its orthodox interpretation.
Time passed leaving youth to recollections.
De Broglie seemed to reconcile himself with his defeat and didn’t grieve much
that his idea about phase harmony passed into oblivion.
25 years later, when de Broglie was slightly
over sixty, the scales fell off his eyes. He understood that ideas of his youth
were significantly richer in content than the present ideas of quantum
mechanics, and the path he had gone before and which he left was in fact the
true and the most promising one. Since that moment a second rise in de
Broglie’s creative life began. He writes numerous papers and publishes a whole
range of books devoted to refutation, criticism and re-interpretation of the
foundations of quantum mechanics (on the whole over 50 papers and 12 books!).
He returns to the ideas of his youth, and begins to examine steadily the
numerous difficult issues which he left out before.
First of all, those devoted to the
composition, structure and internal dynamics of elementary particles as well as
the medium which fills in the inter-particle space and which is necessary for
the existance of stationary waves as their support and propagator. He brings in
the notion of such medium which he calls subquntum medium and models it
as a tachyon gas. Tachyons are the particles with pseudo-mass and super-light
velocity. De Broglie borrowed this idea from the Russian physicist Terletskiy
and used it because he thought it didn’t contradict relatiist postulates.
According to de Broglie, particle is the
most complex system engaged in a constant mass and energy exchange with
environment. It’s a sort of a drop of mist suspended in steam. To describe the
life of such system, particle plus environment, he used thermodynamics methods,
generalizing them and applying at the next hierarchic level of matter
organization. One of his books has this name: ‘Thermadynamics of isolated
particle’ [5]. He thought subquantum medium to be energy containing substance
which he called the ‘hidden thermostat’. In particular, physical and
thermodynamic characteristics of this medium as well as internal
characteristics of elementary particles themselves - they represent the ‘hidden
parameters’ of which there’s so much talk nowadays.
De Broglie began and waged his great battle
alone. He was only helped by youth. He was in the same situation he had been at
the time of his youth, even in more complex one becausae quantum mechanics
theory had long become fully developed, and he himself was not young and occupied
a solid position in scientific world. His colleagues were puzzled. Opinions
became split. Some were welcoming and interested, some neutral, others openly
negative. But it didn’t discourage de Broglie. He worked with enthusiasm and
delight. His new rise was confident and long. The peak of his creative acivity
was during his 70s and 80s. ‘I often ask myself, he told his student G. Lochak
on the eve of his 80th birthday, if the period after seventy was,
from the point of intellectual work, the best period of my life?’
And de Broglie did manage to breach a gap in
the quantum theory bastion which had already became classical, and thus violate
the physicists quiet, stir their minds, instill in them doubt and hope and
thereby spur them into new scientific research. He did succeed in this! He had
no time to complete his theory, though much was done for its development and
substantiation. The concepts of ‘pilot-wave’ and ‘phase harmony’ actually
experienced their revival.
De Broglie pinned much hope on those who
would follow him, urging them to think independently and not to be diverted by
superficial results which produced elegant formulas but revealed little; he
urged them to go ahead relentlessly, penetrating farther and deeper into the
innermost essense of things. He urged all who had a passion for investigation
of the foundations of nature to take a closer look at the law of phase
harmony and discover the deep and crucial mystery hidden in it. He believed
this mystery would soon be discovered and would bring fruit, and he was keen to
pass on his belief and hope to those who walked in his footsteps.
* * *
1.
G. Lochak. “De Broglie’s initial conception of de
Broglie waves”. From book: “The wave-particle dualism”, Dordreht, Holland, 1984.
2.
Louis de Broglie.
“Revolution in physics”. Atomizdat, 1965.
3.
Max Jemmer “Evolution of
quqantum mechanic notions”. Nauka, 1985.
4.
L. de Broglie “Correlation
of Heisenberg’s indefinites”. Mir, 1986.
5.
Broglie, Louis de. “La
thermodinamique de la particule
isolée”. Paris, Gauthier-Villars, 1964.
Back to contents ↑
11. Rhythmodynamics’ place in physics
Science,
a
special kind of cognitive activity aimed at development of objective,
systemically classified and substantiated knowledge about the world.
Physics,
Gk
physika. The major branch of natural science which deals with the forms of
motion of matter, its properties, and with phenomena of non-organic nature.
Classical mechanics
is a branch in physics which determines the laws of motion of macroscopic
bodies whose velocity is much less then the velocity of light in vacuum.
Quantum mechanics is a theory in wave mechanics which determines the method of description
as well as the laws of motion of micro-particles (elementary particles, atoms,
molecules, atomic nuclei) and their systems (crystals, for example) as well as
relation of quantities which characterize particles and their systems with
physical quantities measured directly in macroscopic experiments.
Classical and quantum mechanics methods
of research are ideologically incompatible, therefore these branches of physics
are regarded independent.
Rhythmodynamics
is a theory in
wave physics determining: 1) the role of periodical processes in
formation of natural phenomena and their properties; 2) processes
forming all kinds of motion and properties of macroscopic bodies as
well as micro-particles (atoms, molecules) in any speed regimes.
In the author’s opinion,
rhythmodynamics occupies a place between classical and quantum mechanics
(classical mechanics ↔
rhythmodynamics ↔ quantum mechanics).
Back to contents ↑
Conclusion:
results and perspectives
No nonsense in science, please…
No scientific school can claim to possess
the absolute truth because there is always a possibility to find fault with any
of the system of ideas. In this respect competition between schools looks
strange, to put it mildly, and has nothing to do with the actual science. There
can be no winners in such type of competition – it ‘breeds’ only pseudo-truth
which the winning school introduces into curriculum, thereby strengthening its
supremacy over the defeated opponents.
Another matter are model interpretations
which can coexist peacefully side by side. Because no one knows for sure what
the World actually is, and why It is. Model interpretations allow us to take an
unbiased look and say which of those models reflect most adequately the natural
phenomena under study and therefore would be useful to society in the
foreseeable future. Rhythmodynamics as a method of analysis through geometric
modeling, for example. But what’s the practical use of this rhythmodynamics?
What exactly new has it brought to our knowledge of the surrounding world?
Here’s the gist of it:
1. Provides the logically based interpretation of the negative results
of Michelson’s experiment. The interpretation is based on the phenomenon of
standing waves compression and application of this phenomenon in
electrodynamics of the moving bodies.
2. Within the framework of the wave approach the mechanism of
self-organization of isolated independent elements (oscillators) in system was
developed.
3. Dependence of kinetic energy of the system on the phase displacement
between its elements was found.
4. Relation of the phase displacement between the elements
(oscillators) of the system to the motion of this system in wave medium was
revealed.
5. Interpretation was given of the driving force as internal one which
not only participates in changing of the system’s speed regime, but also
maintains motion, making it rectilinear and uniform. Outwardly such motion
looks like motion by inertia.
6. The means of manipulation of the system’s speed and motion direction
through controlled change of phase relations between the system’s elements were
examined.
7. Relation between the energy flow and frequency difference was found.
The notions of energy flow speed, amplitudeless state of energy were
introduced and defined.
8.
Frequency pulling phenomenon was used to
explain the gravitational interaction.
9.
Connection was explained between the fact of the
fall of the test body in gravitational field and discordance of phase and
frequency relations in this body at the atomic level of its organization.
As for its possible practical
application:
1. Thanks to Rhythmodynamics, a single phase-frequency algorithm is
created within the framework of which the whole range of natural phenomena has
acquired its causal explanation. Opening, as a consequence, new vistas, for
example, propulsion of systems in wave medium space at the expense of
‘internal’ forces. Such propulsion can be actually implemented through the
shift in necessary direction of the system’s energy carcass relative to the
elements of this system. In effect, we are talking about transformation of electric
energy directly into propulsion. All energy industry is based on the reverse:
propulsion →
electricity. Whereas no one prohibits electricity to be
transformed back into propulsion. In future space flights, people would manage
without traditional fuel too.
2. Disclosure of mechanisms ensuring the energy flow leads to
understanding that any motion is, first of all, a flow of localized, in the form
of material bodies, energy. What remains is to find out how to control the
state of this energy inside the body. Such engineering solution would produce
a new quality in the form of a non-jet self-propulsion of a body in required
direction.
3. An experimental model is designed, a prototype of a spacecraft,
(unrealized yet due to absence of resources) which may prove viable in future.
Of course the first such craft will be bulky, clumsy and slow. But if it, or
its modification, manages to reach acceleration of, say 1cm/ señ2, which is a thousand times less than acceleration of a
free fall near the Earth’s surface, in a month (30 days) the spacecraft would
cover the distance of
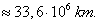 .
.
4.
The rhythmodynamics model
of the processes of the energy flow formation indicate the energy’s ability to
remain in amplitudeless state which opens new prospects in the energy industry.
The exploration of frequency space is also a promising line of research.
The frequency space is as physical as metric one. But this is a next
stage in human exploration of the world of Nature…
Back to contents ↑
Bibliography:
-
Blekhman
I.I. Vibtrational mechanics. Nauka, 1994.
-
Bushuev
V.V. Energy and energy industry. Energia, 2003.
-
Bushuev
V.V., Kopylov I.P. Space and the Earth. Electromechanical interrelations.
Energia, 2005.
-
Veinik
A.I. Thermodynamics of real processes. Minsk. Nauka I tehnika, 1991.
-
Ivanov Y.
N. Rhythmodynamics. Novy tsentr, 1997.
-
Ivanov Y.
N. Rhythmodynamics of amplitudeless fields. Phase-frequency cause of gravitational
drift. Novy tsentr, 2000.
-
Ivanov
Y.N. Compression of standing waves, rhythmodynamics and third state of quiescence.
RIA, 1996.
-
Ivanov
Y.N. Frequency space. Classical mechanics from rhythmodynamics’ perspective.
Novy tsentr, 1998.
-
Detlef Kamke, Klaus
Kramer. Physical foundations of measurement units. Translated from German.
Mir, 1980.
-
Kulakov N.E. Antigravitation
as alternative to jet or heat propulsion. Unpublished paper, posted in the
Internet:
http://www.apvs.narod.ru
-
Kun T. Structure of
scientific revolutions. AST, 2001.
-
Kuper L. Physics for
everyone. Mir, 1974.
-
Logunov A.A. Theory
of gravitational field. Nauka, 2001.
-
Lorentz H., Poincare
A., Einstein A., Minkovskiy G. Relativity principle. Leningrad, ONTI,
1935.
-
Gliozzi M., History
of physics. Mir, 1970.
-
Michelson A.A. Light
waves and their use. Leningrad, 1934.
-
Maxwell J.C. A Treatise
on Electricity and Magnetism. Nauka, 1989.
-
Mach E., Mechanics –
Izhevsk: Regular and chaotic dynamics, 2000.
-
Nevesskiy N.E. Theory
of ether field. Kompania sputnik, 2006.
-
Nikolaev G.V. Scientific
vacuum. Tomsk, Kursiv, 1999.
-
Orear J. Physics.
Translated from English. Mir, 1981
-
Poincare A. On
science. Nauka, 1983.
-
Repchenko O.N. Field
physics. Galereya, 2005.
-
Savrukhin A.P. Origin
of elementary particles and golden section. MGUL, 2004.
-
Spasskiy B.I. History
of physics. Vysshaya skola, 1977.
-
Stavitskiy A.I.,
Nikitin A.N. Speaking the language of nature. Intan, 1997.
-
Whell K., Theory and
experiment in gravitational physics. M, 1997.
-
Foch V.A., Theory of
space, time and gravitation. M, 1961.
-
Frolov A.V. Free
energy. Novaya Energetika Journal, #2, 2003.
-
Chizhov E.B. Spaces.
Novy tsentr, 2001.
-
Chizhov E.B Introduction
into philosophy of mathematical spaces. URSS, 2004.
-
Shipov G.I. Theory
of physical vacuum. Novy tsentr, 1993.
-
Shlyapnikov A.A. Real
abilities of classical physics and false foundations of the modern one. Work
posted in the Internet
http://www.oldhat.narod.ru
-
Einstein A. Collection
of works. Nauka, 1986.
-
Yarkovskiy I.O. Universal
gravitation as a consequence of formation of solid matter inside cosmic bodies.
Kinematic hypothesis. Kushnerov, 1912.
Scientific publishing
Yuri N. Ivanov
Doctor
of Science, Academician of the Russian Academy of Natural
Science, Director of the scientific-technical center STC
"MIRIT"
Rhythmodynamics
(2nd edition, revised and extended)
Official
web-site
http://www.mirit.ru
Board
of editors:
D.N.
Kozhevnikov, V.I. Sidorov, A.I. Shkarubo
Translator:
A.I. Shkarubo
Publishing
House: “Energy”
2007